Vrije klasuren op de randen van het rooster leggen

We illustreren dit probleem met een aantal gevallen uit de praktijk. Er worden op deze pagina verschillende oplossingen in detail uitgewerkt die niet niet alleen nuttig zijn om het probleem op zich op te lossen maar ook om inzicht te verschaffen in de manier waarop men de basisconcepten van Mondriaan kan combineren om roosterproblemen in het algemeen op te lossen.

Op het einde van de pagina kan men de voorbeeldbestanden vinden die gebruikt werden in de tekst.

Probleemstelling

Af en toe kan het niet anders dan dat we klasroosters moeten maken waarbij er meer uren in het rooster zitten dan dat er les gegeven moet worden. In dergelijke gevallen hebben we het probleem van de vrije uren. De vraag die dan beantwoord moet worden is waar we die vrije uren moeten/mogen inplannen. Wat meestal niet handig is, is dat er springuren ontstaan in het midden van een dag. Een betere oplossing is om ze aan het einde van een dag te leggen, aan het begin van een dag, of dat er een combinatie van beide toegelaten is. Op deze pagina zullen we een aantal praktijkvoorbeelden bekijken samen met de oplossingen die gebruikt werden.

We behandelen volgende voorbeelden:

• Voorbeeld 1 – Klassen met 33 uur les op een rooster van 35 uur (2 vrije uren te plannen)
  • Oplossing 1: we gebruiken énkel waardespreidingen. De vrije uren worden niet als aparte opdrachten geplaatst.
  • Oplossing 2: de vrije uren worden als aparte opdrachten ingevoerd. We gebruiken blokjes van 1 en van 2 uur met een techniek van overloop-resources om de keuze tussen blokjes van 1 of 2 uur te maken. Dit gaat in combinatie met een eenvoudige waardespreiding.
• Voorbeeld 2 – klassen met 33 uur les op een rooster van 41 uur en een variabele middagpauze (4 vrije uren te plannen)
  • Oplossing 1: we plaatsen de vrije uren als individuele opdrachten van 1 uur en drijven ze naar de randen via volgordespreidingen.
  • Oplossing 2: we plaatsen de vrije uren als individuele opdrachten van 1 uur en drijven ze per dag ofwel naar de bovenrand ofwel naar de onderrand via volgordespreidingen.

Voor elke van de 3 oplossing wordt het Mondriaan bestand meegeleverd.

Voorbeeld 1 – Klassen met 33 uur les op een rooster van 35 uur

We hebben een aantal klassen die 33 uur les hebben maar waarvoor het onmogelijk is om die 33 uur op een vast rooster van 35 uur te plannen. Door beperkingen die ontstaan door samenzettingen van klassen, lokalenproblematiek, beschikbaarheid van leerkrachten werd besloten om meer ruimte in het rooster te voorzien. Door 2 extra uren op te nemen in de roosterruimte ontstaat er meer zuurstof om de opdrachten te kunnen plannen. Door het invoeren van 2 extra uren in het rooster ontstaat wel het probleem van “springuren”. De vraag is of we die springuren niet kunnen vermijden door ze aan de bovenrand van het rooster te leggen zonder afbreuk te doen aan het vinden van een mogelijk oplossing voor het rooster.

Het rooster dat in dit voorbeeld gebruikt wordt is typisch een 5-daags rooster waarbij woensdagnamiddag vrij is. Voor maandag, dinsdag en donderdag worden 8 uur voorzien, voor vrijdag maar 7. Dat er op vrijdag liever niet tot het 8ste uur wordt gewerkt is een logische keuze. Er zijn dus 35 roosterpunten mogelijk waarop we 33 lesuren moeten plannen.

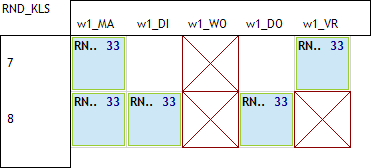
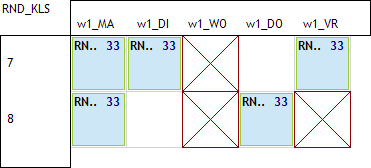
Volgende 3 plaatjes tonen mogelijke oplossingen waarbij de eerste niet aanvaardbaar is. In het tweede voorbeeld liggen de vrije uren op de rand en hebben we dus geen springuren. In het derde voorbeeld hebben we op donderdag 2 vrije uren op 7 en 8 wat ook aanvaardbaar is.

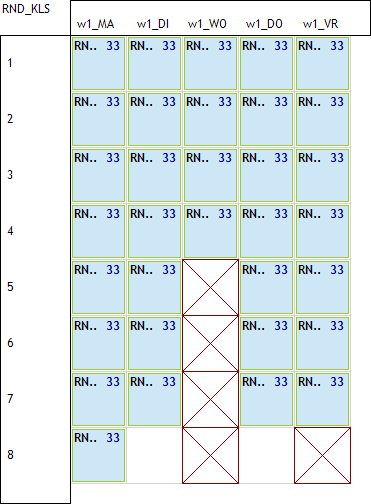
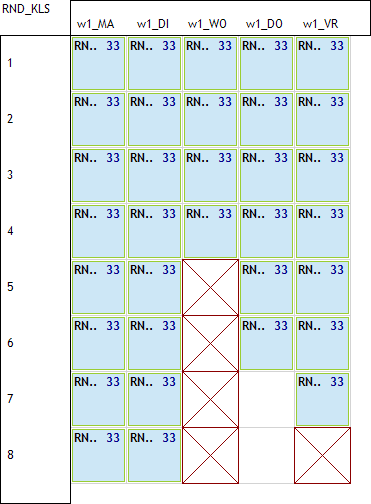
Voor elke klas kan de oplossing anders zijn maar de regel is dus eenvoudig. De 2 vrije uren liggen

• ofwel als 2 losse uren op ma8, di8, do8, vr7
• ofwel als “blokje” van 2 uur op ma7, di7, do7

Het is in dit voorbeeld niet toegelaten om een blokje van 2 vrije uren op vr6 te hebben. Dus, de 2 vrije uren liggen hoe dan ook op het het 7de en/of 8ste uren. We gaan ons dus focussen op dit deel van het rooster:

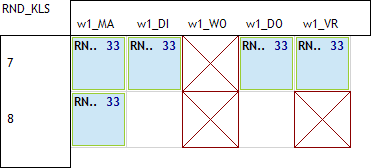
Oplossing met enkel spreidingsregels

Een mogelijke oplossing is om dit aan te pakken is via extra waardespreidingen. Dit vraagt wel wat denkwerk maar eens het patroon gekend is kan men variaties maken op het thema.

In de spreidingsregels die we hier uitleggen bevat de groep “Klassen-33u” alle klassen die aan deze regels moeten voldoen. De beschreven spreidingsregels zullen voor elke individuele klas uit deze groep gelden.

We beginnen met het forceren van de vrije uren naar het 7de en 8ste uur van de week. De manier om dat te doen via een spreiding is te stellen dat er maximum 5 uur les gegeven kunnen worden op deze uren. Als er maar 5 uur op de 7de en 8ste uren gegeven mogen worden dan kan het niet anders dan dat de 2 vrije uur daar komen liggen.

Het gaat om de eerste spreidingsregel. Voor elke klas maximaal 5 uur les op de uurlijst “ZevendeAchtste” die alle 7de en 8ste uren van het rooster bevat.

Een volgende beperking die we kunnen opleggen is eisen dat er maximaal 2 uur les op het 8ste uur gegeven wordt. Van zodra er 3 uur les gegeven wordt op het 8ste zijn we zeker dat er een springuur ontstaat (wetende dat er 5 uur op het 7de en 8ste gegeven wordt). We illustreren dit hier met een voorbeeld. We leggen 3 uur op het 8ste en wetende dat er 5 uur op het 7de en 8ste kunnen liggen kan het niet anders zijn dat dat er 1 of 2 springuren vallen op het 7de uur:

De eis dat de klassen maximaal 2 uur les hebben op het 8ste vertaalt zicht in de tweede spreidingsregel. De uurlijst “Achtste” is als volgt gedefinieerd:

Deze 2 spreidingsregels zijn nodige maar nog niet voldoende voorwaarden om te bekomen wat we graag hebben. Er zijn namelijk gevallen waarbij aan beide spreidingen voldaan is maar waarvoor nog steeds foute oplossingen kunnen bestaan. Volgend voorbeeld voldoet aan de 2 spreidingsregels maar is nog steeds fout omdat we een springuur hebben op do7:

We moeten de gevallen systematisch trachten te identificeren die nu fout kunnen gaan. Voor elk van die gevallen kunnen we dan een oplossing formuleren.

Voor het 8ste uur zijn er 2 mogelijkheden: ofwel staat er 1 uur, ofwel staan er 2 uren. Geen les op het 8ste is niet mogelijk en meer dan 2 ook niet. Kan er iets misgaan als er op het 8ste uur maar 1 uur les is? Neen. Als er op het 8ste uur maar 1 uur les is dan moeten de 7de uren allemaal gevuld zijn met lessen en liggen de vrije uren dus op het 8ste. Er kan dus alleen iets misgaan indien er exact 2 uur les gegeven wordt op het 8ste. Komt overeen met het voorbeeld dat hierboven gegeven is. Laat ons de foute situaties eens bekijken voor het geval dat er 2 uur op het 8ste staan. Stel dat er géén les gegeven wordt op vr7:

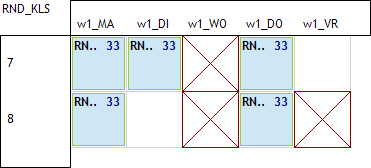
Als er geen les op vr7 is dan kan het niet fout gaan. Dus, de enige foute situaties kunnen maar ontstaan op voorwaarde dat er op vr7 wél les gegeven wordt er dat er op het 8ste 2 uur les gegeven wordt. We bekijken de mogelijke situaties waarbij vr7 les heeft en waarbij er op het 8ste 2 uur les zijn en het fout gaat:

geen les op do8:

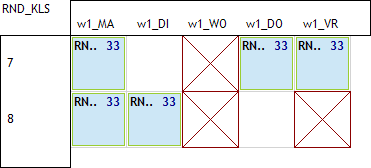
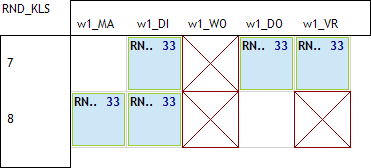
geen les op di8:

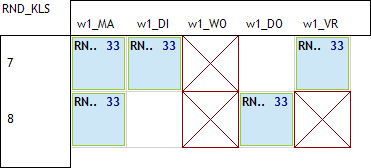
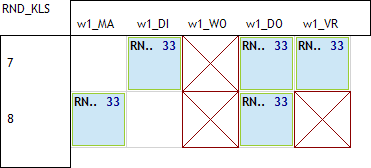
geen les op ma8:

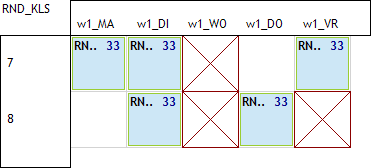
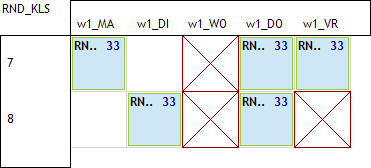
Dit zijn de 6 combinaties die nog mis kunnen gaan als we enkel de eerste 2 spreidingsregels gebruiken. Een eerste manier om dit op te lossen is op een eenvoudige manier deze 6 combinaties verbieden via spreidingsregels. Stel dat we de eerste willen vermijden via een waardespreiding:

• Maak een EN-uurlijst (bv U33-Fout-01) met de volgende 5 uren: ma7, ma8, di8, do7, vr7
• Maak een waardespreiding voor Klassen-33u die stelt dat je maximum 4 uur mag bezetten op U33-Fout-01
• Door dit te zeggen wordt nooit toegestaan dat op die 5 uur ook 5 uur lesgegeven wordt.

Dit kunnen we herhalen voor elk van de 6 combinaties. We gebruiken dan volgende uurlijsten:

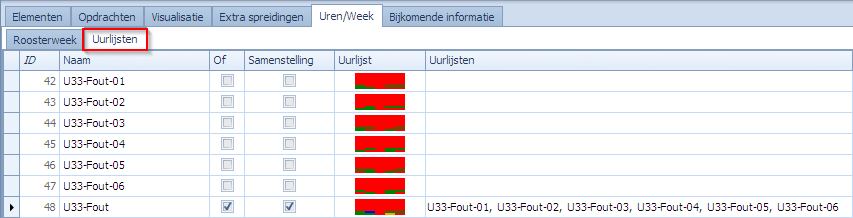
De spreiding om de foute combinaties te vermijden voor alle klassen wordt dan:

Dit geeft een perfect oplossing voor het probleem. Echter, als men het probleem nog eens in detail bekijkt zal men zien dat het korter kan, met minder spreidingsregels. Bekijken we bijvoorbeeld terug de eerste 2 combinaties waarbij geen les op do8 gegeven wordt:

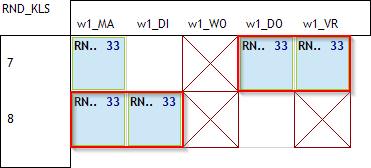
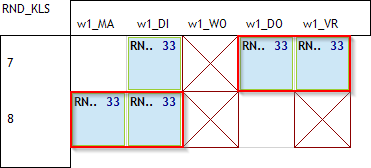
In beide gevallen die hier fout gaan zien we dat we het al kunnen weten door te kijken naar ma8, di8, do7, vr7. Van zodra er op deze 4 uur lesgegeven wordt zal het fout gaan, eender waar het 5de uur geplaatst wordt (ma7 of di7). Hetzelfde kunnen we toepassen op de 4 andere gevallen. Passen we dit toe dan herleiden we het probleem naar in totaal 3 foute combinaties die we in een waardespreidingsregel kunnen opnemen. Dit zijn de 3 combinaties. De rode cirkels geven aan waar het 5de uur fout geplaatst zou worden.

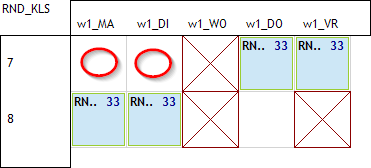
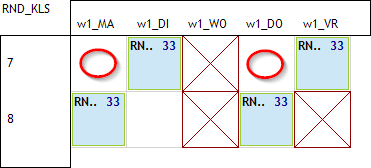
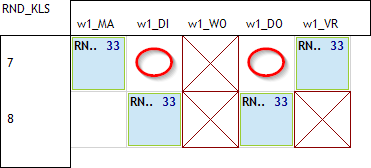
We hebben dus 3 uurlijstjes nodig met telkens 4 uur waarop we de spreiding gaan definiëren:

Dat brengt ons dan terug bij de spreidingsregel die we eerder toonden.

We stellen dat er maximum 3 uur gepland mogen worden op de uurlijstjes vervat in U33. Van zodra er een 4de uur bijkomt weten we zeker dat het fout gaat.

Om nog wat meer inzicht te krijgen in de manier waarom men met waardespreidingen deze problemen kan oplossen hebben we in volgend MS Excel bestand een heel aantal voorbeelden opgenomen. Het gaat om het plannen van vrije uren op het 7de en 8ste uur van een basisrooster. De voorbeelden gaan van 1 vrij uur tot 7 vrije uren die moeten voorzien worden op de rand.

• Randuren oplossen door waardespreidingen – Enkele voorbeelden

Oplossing met het plaatsen van randblokjes en waardespreidingen

Een andere oplossing om springuren te vermijden en de vrij uren dus naar de randen van het rooster te drijven is door de vrije uren als extra opdrachten voor de klassen in te voeren. Men maakt de vrije uren expliciet en plaatst ze als het ware mee in het rooster. Dergelijke opdrachten zullen dan in principe enkel de klas als resource bevatten en een uurlijst waar de de vrije uren mogen staan. Als vak zou men bijvoorbeeld RAND kunnen meegeven om gemakkelijk te selecteren en om duidelijker het onderscheid te kunnen maken in het rooster.

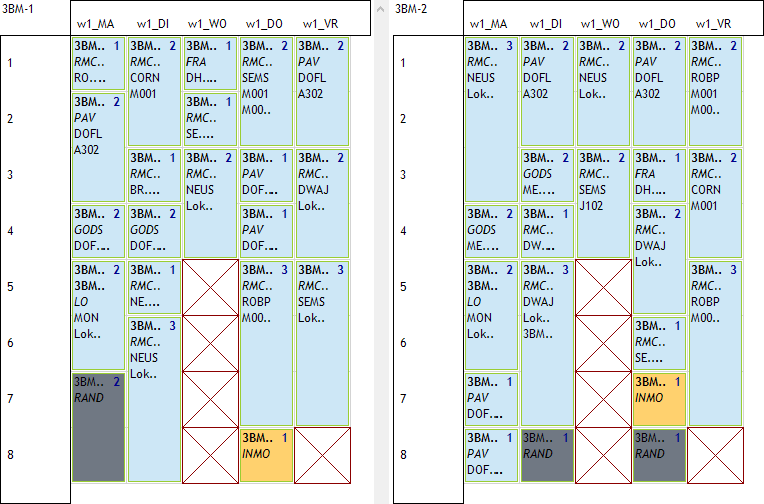
In volgend voorbeeld zien we 2 klassen waarvoor we de vrije uren als blokjes op de rand gelegd hebben. Voor de klas links hebben we 2 vrije uren na elkaar op dinsdag 7 en 8. Voor de klas rechts hebben we maandag 8 en vrijdag 7 als vrije uren op de rand.

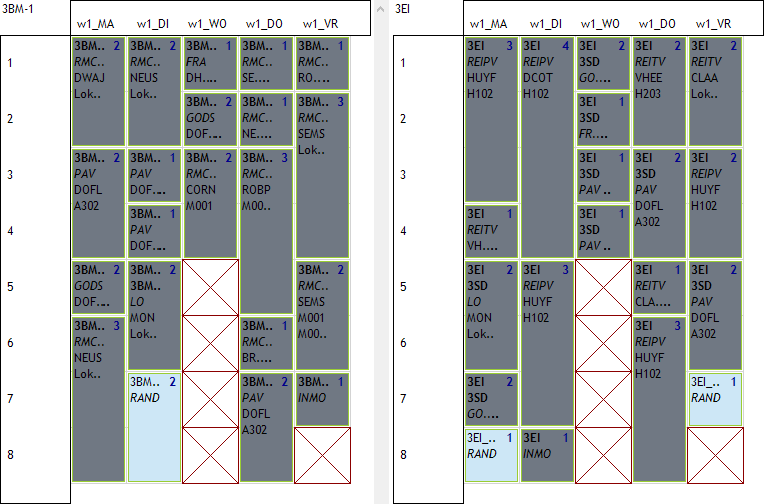
Op het eerste zicht lijkt dit een gemakkelijke oplossing te zijn maar dat is het niet. Het feit dat links een blokje van 2 op di7 staat en rechts 2 lossen blokjes op ma8 en vr7 illustreert het probleem al. Om de vrije uren op een correcte manier te plaatsen hebben we:

• ofwel 2 losse vrije uren nodig die op ma8, di8, do8, vr7 kunnen staan
• ofwel een blokje van 2 vrije uren die op ma7, di7, do8 kunnen staan

Mondriaan ondersteunt (momenteel) nog geen opdrachten die op deze manier uren kunnen plaatsen (2 uur plaatsen als ofwel 2 losse op een bepaalde uurlijst, ofwel als blok op nog een andere uurlijst). We gaan dus een manier moeten vinden om dit via een omweg toch te doen. (Merk op dat we verder op deze pagina in Voorbeeld 2 een andere techniek bekijken om hetzelfde te bereiken.)

Er zijn verschillende manieren om dat te doen waarvan we er hier één bekijken.

We beginnen met de uurlijsten waarop de vrije uren geplaatst mogen worden:

• RND_33_1 voor lossen vrije uren
• RND_33_2 voor de blokjes van 2 vrije uren na elkaar

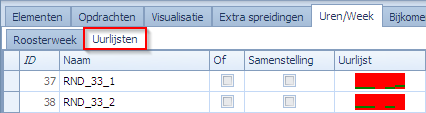
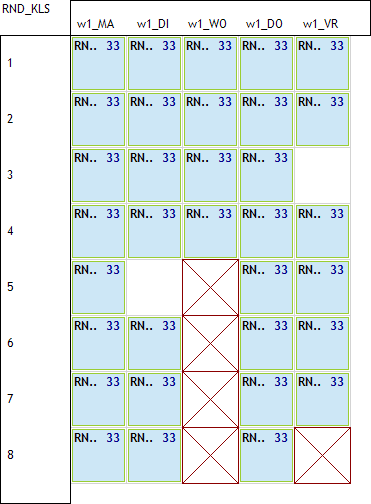
Wat we willen bekomen is dat er voor elke klas ofwel 2 losse vrije uren geplaatst worden op RND_33_1, ofwel een blokje van 2 uur op RND_33_2. Stel dat we voor elke klas 3 opdrachten voorzien om dit te doen. Als voorbeeld nemen we de klas 3BM-1:

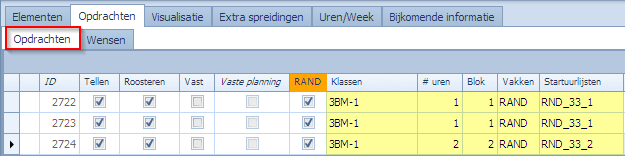
We hebben hier de juiste blokjes op de juiste uurlijsten maar het probleem is dat we nu niet 2 maar 4 vrije uren in het rooster proberen te plaatsen. Dit is niet de bedoeling en gaat ook niet lukken. We moeten een manier vinden om via deze 3 opdrachten exact 2 vrije uren te plaatsen in 3BM-1 zonder dat een van de opdrachten faalt. Het systeem zou dan moeten kunnen kiezen tussen ofwel 2 losse uren, ofwel het blokje van 2 vrije uren.

Een manier om dat te doen is door een “overloop” resource te voorzien. We gaan de 4 vrije uren niet alleen in 3BM-1 plaatsen maar we gaan elk van de opdrachten ook de mogelijkheid geven om ze op een ander rooster te plaatsen, een overloop rooster. Als we elke opdracht kunnen laten kiezen tussen 3BM-1 en bijvoorbeeld de overloop resource RND_3BM-1 dan kan dat wel lukken. Enige wat we dan nog wel moeten doen is er voor zorgen dat niet alle vrije uren naar de overloop resource gaan. Via een eenvoudige waardespreiding kunnen we dat beperken tot exact 2. Als zowel 3BM-1 als RND_3BM-1 2 vrije uurtjes krijgen dan is het opgelost.

Volgende 2 plaatjes tonen het resultaat voor de klassen die we eerder gebruikten.

Voor 3BM-1 gebruiken we de overloop resource RND_3BM-1 (als dummy klas gedefinieerd).  Hier zien we dat de echte klas het blokje van 2 gekregen heeft en de overloop resource heeft de 2 losse uren gekregen.

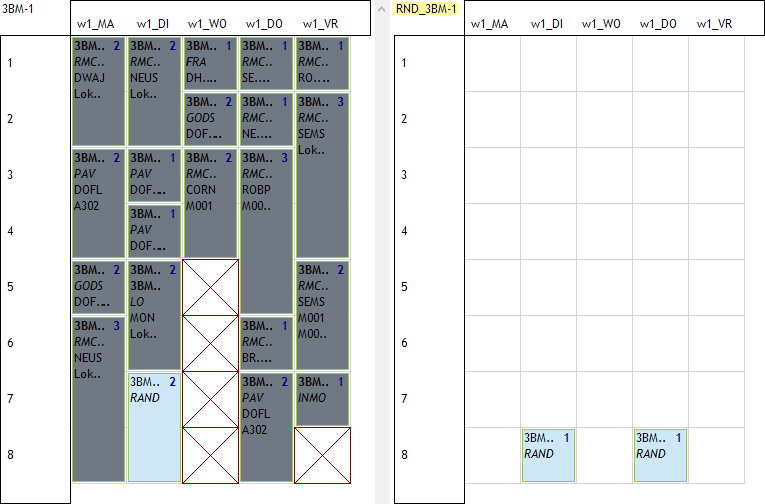
Voor 3EI gebruiken we de overloop resource RND_3EI (als dummy klas gedefinieerd). Hier zien we dat de echte klas de 2 losse uren gekregen heeft en de overloop resource heeft het blokje van 2 gekregen.

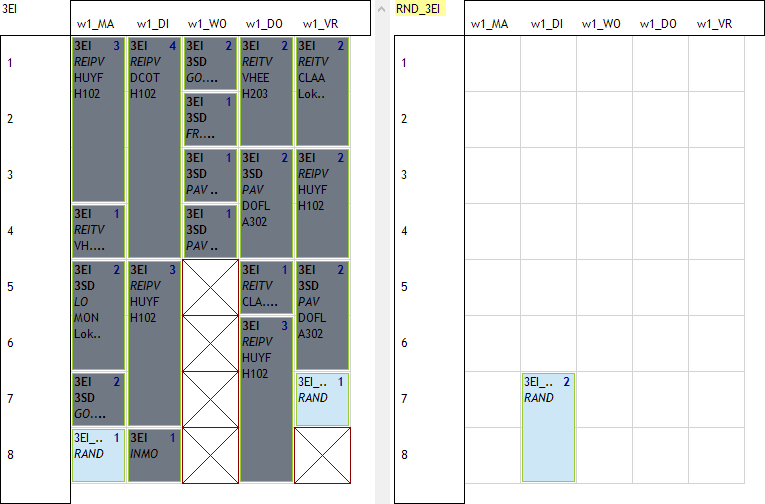
We bekijken nu wat we verder nodig hebben om dit systeem op te zetten.

Als overloop resources definiëren we voor elke klas een dummy klas met als prefix bijvoorbeeld “RND” om het onderscheid met de echte klassen te bewaren.

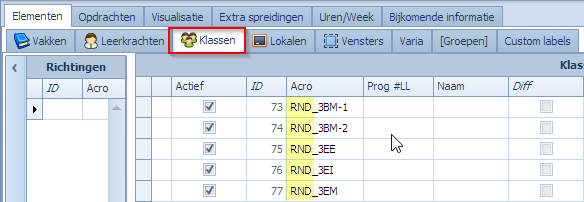
Voor elke klas maken we een OF-klasgroepje waarin de klas en zijn overloop resource zit. Deze groepjes gaan we kunnen gebruiken in de opdrachten voor de vrije uren. Elk van die opdrachten kan dan kiezen uit ofwel de echte klas, ofwel de overloop resource.

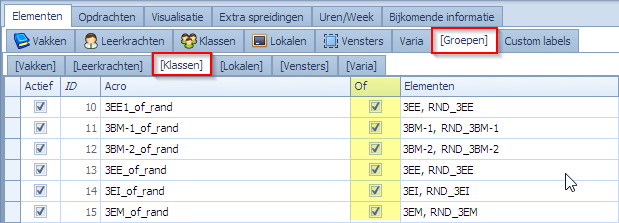
Om de waardespreiding op een eenvoudige manier te kunnen definiëren maken we ook nog een klasgroep aan waarin alle overloop resources zitten.

Vervolgens maken we de opdrachten aan voor iedere klas om de vrije uren te plannen. Als klas gebruiken we telkens het OF-groepje dat kan kiezen tussen de echte klas of de overloop resource.

Tenslotte willen we voorkomen dat voor een klas de vrije uren allemaal naar de overloop resource gaan. Dat doen we door een waardespreiding. Die gaat voor elke overloop resource tellen hoeveel uren er over gans de week (w1) geplaatst zijn. Die telling mag niet meer dan 2 opleveren. Niet meer dan 2 zal door de andere beperkingen in het systeem resulteren in exact 2.

Kan dit ook via variatypes in plaats van met een dummy overloopklas?

Enkel de dummy overloopklas vervangen door een variatype is niet mogelijk. De reden is dat we in een opdracht niet toelaten dat er gekozen wordt tussen een klas en een variatype. In de kolom “Klassen” kan men enkel klassen en groepen van klassen opnemen. Het is niet mogelijk om een groepje te maken van een klas en een variatype.

Wat wel zou kunnen is dat men 2 variatypes gaat gebruiken in de opdrachten voor de vrije uren. Voor elke klas maakt men dan 2 variatypes aan (bijvoorbeeld “V_<klas>” en “V_<klas>_overloop”) die de 2 blokjes van 1 uur en het blokje van 2 uur onderling verdelen. Dat is uiteraard niet voldoende omdat er dan geen koppeling meer is met die klas. Om de koppeling te maken zet men dan in elke lesopdracht van de klas het extra variatype “V_<klas>”.

Kan dit ook zonder een overloop resource?

Inderdaad, er is ook een oplossing mogelijk zonder deze overloop resources. Als men gebruik maakt van volgordespreidingen in plaats van waardespreidingen kan men het zonder deze constructie doen. Een dergelijke oplossing wordt besproken in Voorbeeld 2.

Vergelijking tussen beide oplossingen voor Voorbeeld 1

De oplossing met de spreidingen is moeilijker te begrijpen en op te stellen. Van zodra er variaties zijn in de hoeveelheid vrije uren en de structuur van de week moeten de spreidingen en bijhorende uurlijsten weer systematisch opgebouwd worden.

De oplossing met de expliciete blokjes is eenvoudiger van opzet en ook gemakkelijker aan te passen indien er variaties zijn.

Qua rekentijd is gebleken dat de oplossing met enkel spreidingen meestal te verkiezen valt boven de oplossing met de te plaatsen vrije uren. De keuze is aan de gebruiker. Uiteraard zijn er ook nog andere oplossingen te bedenken en dat is juist de kracht van Mondriaan. Via een aantal krachtige basisconcepten kan men erg veel constructies bedenken die tot een oplossing leiden. Het is goed om hier de nodige experimenten mee te doen.

Extra bonus in voorbeeldbestand – Inhaalmomenten op het einde van de dag

In de voorbeeldbestanden voor beide oplossingen werd ook nog een interessante constructie gebruikt voor het plannen van inhaalmomenten. Een inhaalmoment is een uurtje les op het einde van de dag. De klastitularis kan beslissen welk vak op dat moment gegeven wordt en aan welke leerlingen. Omdat niet alle leerlingen alle inhaalmomenten moeten volgen worden de inhaalmomenten aan het einde van de dag gepland. De leerlingen die er dan niet hoeven te zijn kunnen dat naar huis. In volgend voorbeeld zien we voor klas 3BM-1 dat het inhaalmoment op do8 valt en voor 3BM-2 op do7 (oranje ingekleurd). Het getoonde voorbeeld komt uit het bestand waar de vrije uren met opdrachten wordt opgelost.

Inhaalmomenten (vak INMO) zijn opdrachten die 1 uurtje plannen op het 7de of 8ste uur van de dag. Wat we willen afdwingen is dat de inhaalmomenten nooit voor een les vallen. Als er een inhaalmoment is, dan moet het op het einde van de dag komen. Het enige wat potentieel mag volgen op een inhaalmoment is een vrij uurtje (vak RAND).

In volgend overzicht ziet men de opdrachten  voor de klas 3BM-1. Het inhaalmoment (vak INMO) is een blokje van 1 uur dat op het 7de of 8ste uur kan liggen. We hebben nu ook een custom kolom ingevoerd (O_TYPE) van het type “lijst” met de waarden (LES, INHAAL, VRIJ). We hebben de opdrachten opgedeeld in deze kolom volgens hun type (voor alle klassen waarvoor dit nodig is). We gaan dit nodig hebben voor de spreidingen die moeten afdwingen dat INMO het laatste vak van de dag wordt.

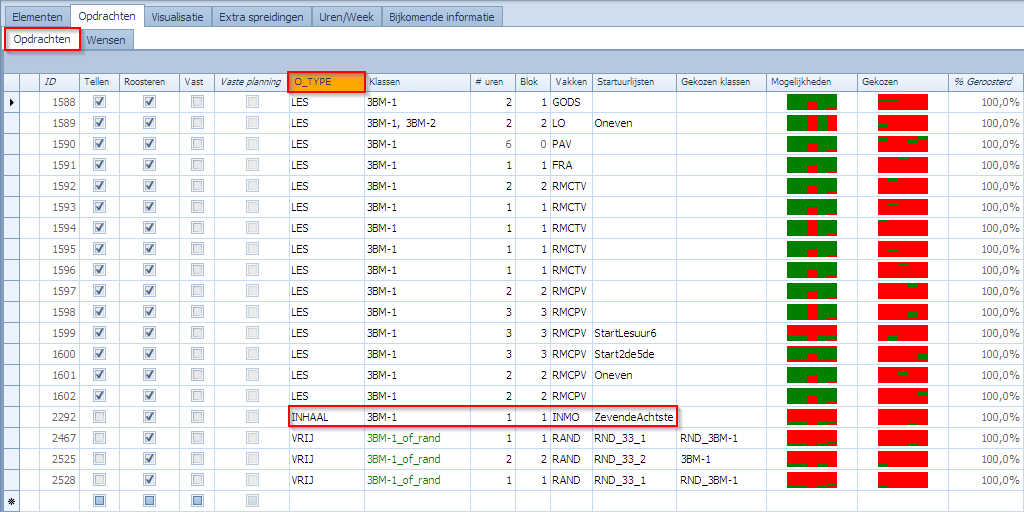
Hoe kunnen we nu afdwingen dat INMO voor een klas het laatste vak van de dag is? Door de uurlijst die we met INMO meegeven (ZevendeAchtste) weten we al zeker dat het uur op het 7de of 8ste uur van de dag valt. Dat is al goed maar nog niet voldoende. Op het 7de en 8ste uur kan ook nog gewoon les vallen en er kunnen ook vrije uren vallen. Om dit op te lossen moeten we een spreidingen definiëren. Bekijken we maandag:

• Als INHAAL en LES voorkomt in het tijdsinterval [ma7, ma8] voor 3BM-1 dan moet INHAAL steeds na LES volgen.

Dit moeten we kunnen zeggen voor maandag, dinsdag, donderdag en vrijdag. We hebben hiervoor een aantal uurlijsten nodig.

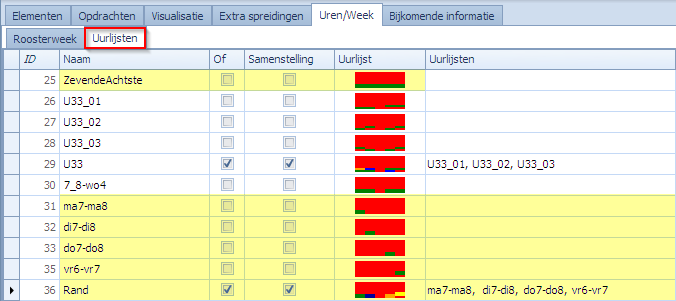
De uurlijst “Rand” bevat 4 sub-uurlijstjes van telkens 2 uur. Ze stellen de intervallen voor waarbinnen we de volgordespreidingen gaan laten gelden. Bijvoorbeeld ma7-ma8 is het sub-uurlijstje dat het interval [ma7, ma8] definieert.

Als we dan volgende volgordespreiding definiëren voor 3BM-1 dan zal INMO steeds na LES komen, op eender welk van de 4 dagen.

Bekijken we de eerste spreiding (voor 3BM-1) dan zitten daar volgende elementen in:

• Selectie 1: definieert een eerste set opdrachten: alle opdrachten waar én 3BM-1 inzetten én waarvoor de custom-kolom O_TYPE de waarde INHAAL heeft. Merk op  dat het én is (“En Selectie 1” aangevinkt)
• Selectie 2: definieert een tweede set opdrachten: alle opdrachten waar én 3BM-1 inzetten én waarvoor de custom-kolom O_TYPE de waarde LES heeft. Merk op  dat het én is (“En Selectie 2” aangevinkt)
• Type: “Na”. Dit betekent dat alle opdrachten uit Selectie 1 NA de opdrachten uit Selectie 2 moeten komen.
• Uurlijsten: “Rand” is een OF-uurlijst van 5 uurlijsten die elk op hun beurt een interval definiëren. Dus, de volgordespreiding geldt nu in elk van die 5 intervallen.

Merk op dat we de opdrachten waarvoor O_TYPE = VRIJ niet meenemen in deze volgordespreiding. Moesten we die vrije uren bijvoorbeeld als LES behandelen dan konden we nooit een inhaalmoment en een vrij uur op dezelfde dag hebben. Vandaar dat we de opdeling gemaakt hebben via een custom-kolom. Merk op dat we in het oplossing met enkel spreidingen dit probleem van de vrije uren in combinatie met inhaalmomenten niet hebben omdat ze daar niet expliciet als opdrachten bestaan. Daar hoeven de volgordespreidingen voor de inhaalmomenten geen rekening te houden met de vrije uren.

Voorbeeld 2 – Klassen met 33 uur les op een rooster van 41 uur

In dit voorbeeld hebben we klassen die 33 uur les hebben op een rooster van 41 uur. Het gaat om klassen met een variabele middagpauze. Vanwege bepaalde beperkingen in de school is het niet mogelijk om iedereen op hetzelfde moment in middagpauze te laten gaan. In dat geval is het nodig om de middag mee in het rooster op te nemen. De middagpauze gaat door op het 5de of 6de uur. Blijkbaar is een variabele middag nog niet voldoende om alle lessen gepland te krijgen en heeft de school beslist om per klas 4 uur extra te voorzien waarop geen les gegeven wordt. Er ontstaan in elke klas 4 vrije uren. De vrije uren mogen niet overal liggen. De regels die de school oplegt zijn de volgende:

• De vrije uren mogen op eerste 2 uur van elke dag liggen (ma1, ma2, di1, di2, wo1, wo2, do1, do2, vr1, vr2).
• De vrije uren mogen op de laatste 2 uur van elke dag liggen (ma8, ma9, di8, di9, wo4, wo5, do8, do9, vr8, vr9).
• Er mag geen vrij uur na een lesuur liggen op dezelfde dag.

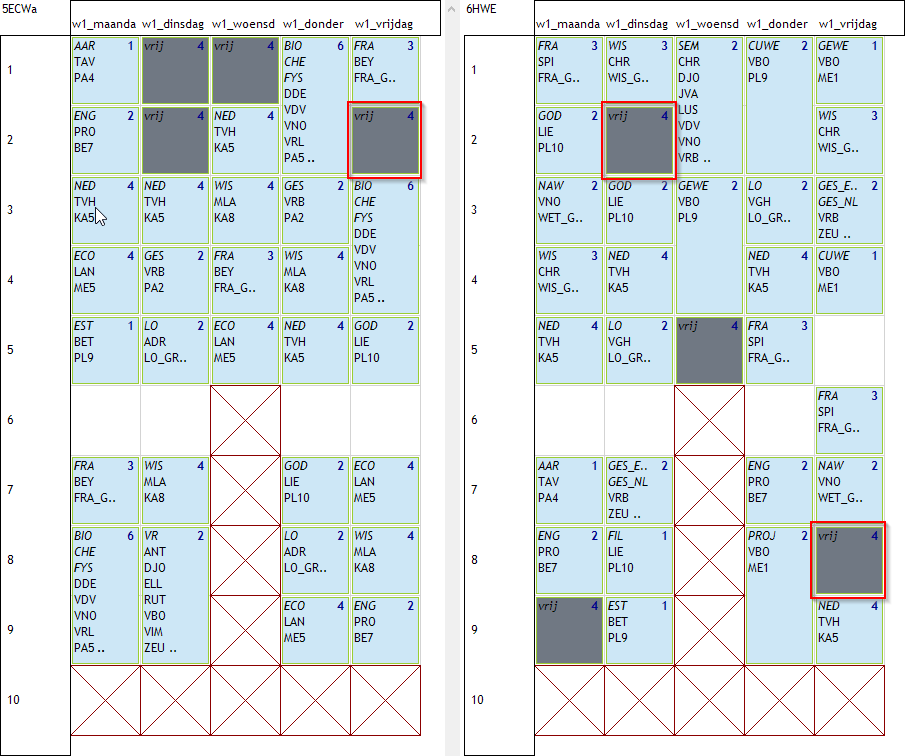
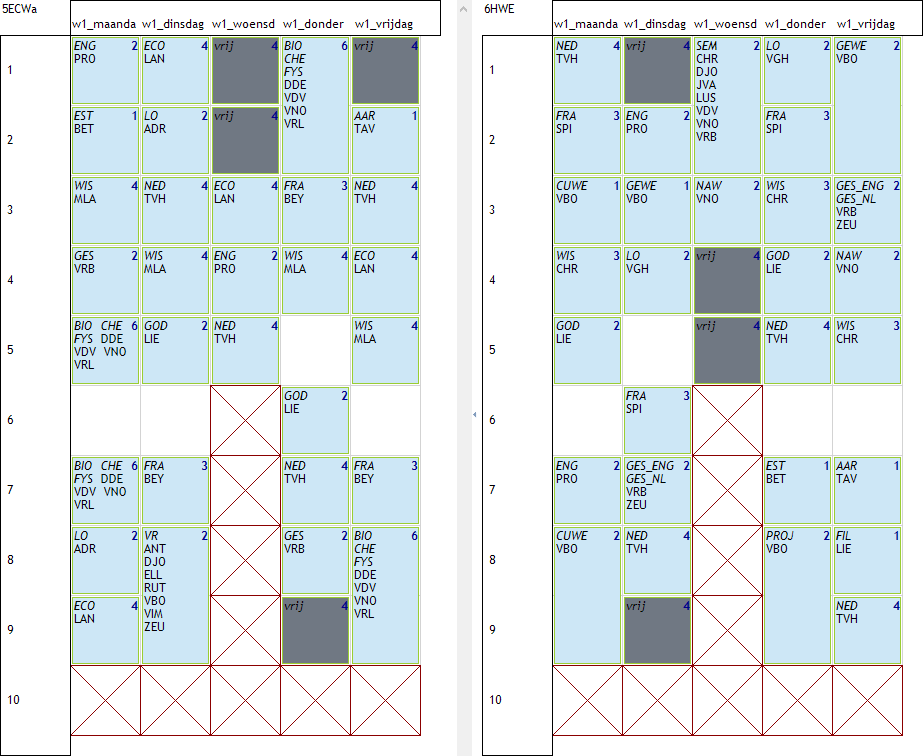
In volgend voorbeeld zien we 2 klassen met telkens 4 vrije uren die aan deze regels voldoen. Zie ook de lege plaatsen die de middagpauze voorstellen.

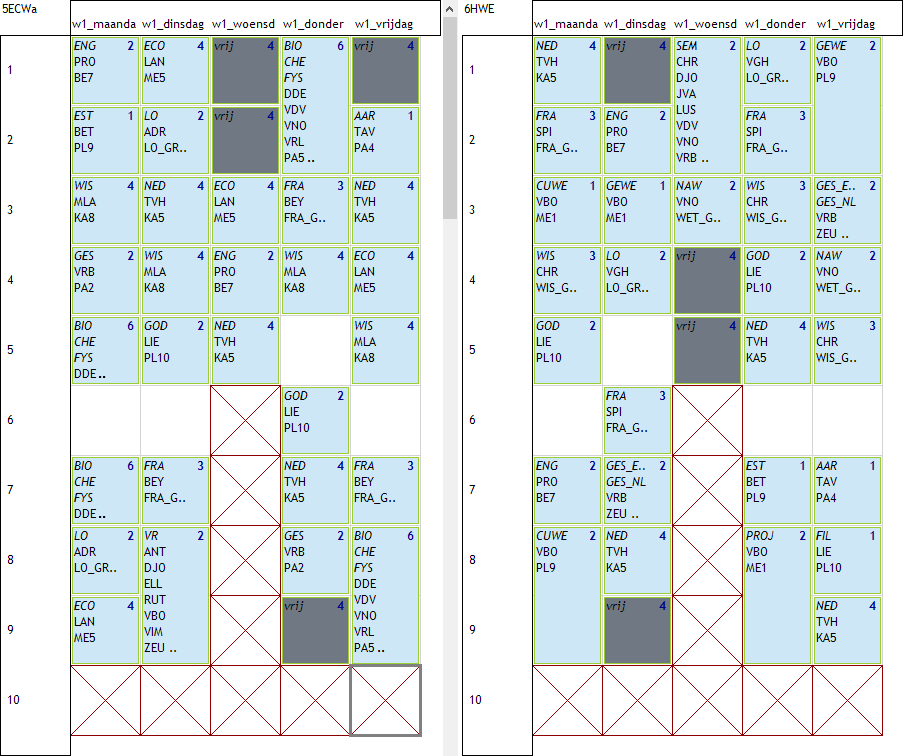
Het plannen van een variabele middagpauze is niet echt het onderwerp van deze pagina maar laat ons dat eerst even bekijken voor we aan de vrije uren beginnen. Het probleem speelt zich af op het 5de en 6de uur van maandag, dinsdag, donderdag en vrijdag. Voor alle klassen moet gelden dat ze op elk van die dagen ofwel het 5de ofwel het 6de uur geen les hebben. Het is niet de bedoeling om daar de vrije uren te leggen, we gaan die momenten gewoon leeg roosteren. Dit kan eenvoudig door een waardespreiding. Als we bijvoorbeeld op de uren (ma5, ma6) tellen hoe vaak de klas 5ECWa daar gepland is dan mag dat maximum 1 uur zijn.

We hebben hiervoor volgende uurlijsten nodig.

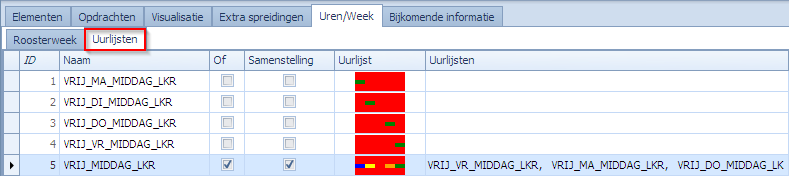
Voor elke middag een uurlijstje van 2 uur en de OF-uurlijst VRIJ_MIDDAG_LKR zet deze samen om er handig gebruik van te kunnen maken in de waardespreidingen. Deze uurlijsten bevatten LKR in hun naam omdat ze oorspronkelijk bedoeld waren om enkel leerkrachten een middagpauze te kunnen geven maar ze kunnen evengoed voor de klassen gebruikt worden.

Ook is het handig om een groep van klassen te hebben zodat we de spreiding kort en bondig kunnen noteren. GR3 is een EN-groep van alle klassen waarvoor we de middagpauze moeten regelen. De spreidingsregel wordt dan:

Voor elke klas in GR3 en voor elk koppel van 5de en 6de uren eisen we dat er maximaal 1 uur gepland is. Dat lost het probleem van de variabele middagpauze op voor de klassen. Voor de leerkrachten wordt het trouwens op gelijkaardige wijze geregeld op volgende manier:

Merk op dat we voor leerkrachten als extra selectiecriterium LES gebruiken. Dit verzekert dat we geen wensopdrachten of eventueel optimalisatieopdrachten meenemen in de spreiding en dus enkel lesopdrachten. LES is criterium dat de gebruiker zelf niet kan manipuleren. Elke opdracht in het opdrachten tabblad is LES. Het gaat in dit geval dus niet om een custom kolom maar om een systeemlabel.

Oplossing met losse blokjes en volgordespreidingen

Nu de middagpauze geregeld is kunnen we de 4 vrije uren gaan plannen als randuren. In Voorbeeld 1 hadden we al een voorbeeldoplossing gezien met enkel waardespreidingen en ook een met het expliciet plaatsen van blokjes in combinatie met een overloop resource en waardespreidingen. Hier gaan we het op weer een andere manier aanpakken. We gaan de 4 blokjes allemaal als aparte uren plannen en via een volgordespreiding ervoor zorgen dat ze naar de randen gedreven worden.

Eerst beslissen we waar de randblokjes mogen liggen. Wat we weten moeten we niet overlaten aan Mondriaan. Als we weten dat het niet anders kan dan dat de randblokjes op de randen moeten liggen dan kunnen we dat ook best vastleggen. Ook indien andere beperkingen er automatisch voor zouden zorgen dat ze naar de randen gedreven worden is het toch nuttig om het expliciet te maken. Voor alle klassen moeten de randblokjes op volgende randen liggen:

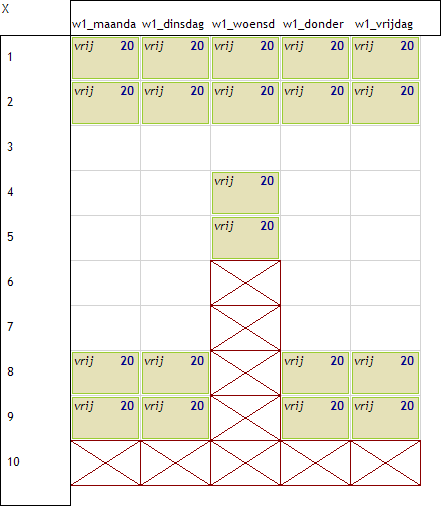
De uurlijst RAND definieert deze uren. Alle opdrachten die vrije uren plaatsen zullen met deze uurlijst werken.

Bekijken we de opdrachten voor klas 5ECWa. De vrije uren worden hier gewoon als 1 opdracht van 4 uur opgevoerd. Het vak is “vrij” en de uurlijst is “RAND”. Merk op dat we in het tabblad een custom kolom (vlagje) “LES” hebben toegevoegd. Voor de opdrachten die echt les zijn is dit aangevinkt. Voor de vrije uren is het uitgevinkt. Verwar in dit voorbeeld de custom kolom “LES” niet met de systeemlabel LES die Mondriaan standaard aan alle opdrachten uit het tabblad “Opdrachten” toekent.

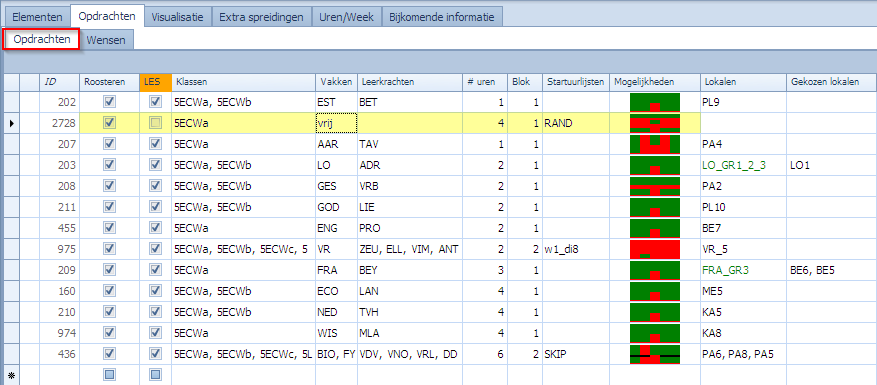
Zetten we het filter op “vrij” dan zien we alle opdrachten om vrije uren te plannen voor alle klassen die dat nodig hebben.

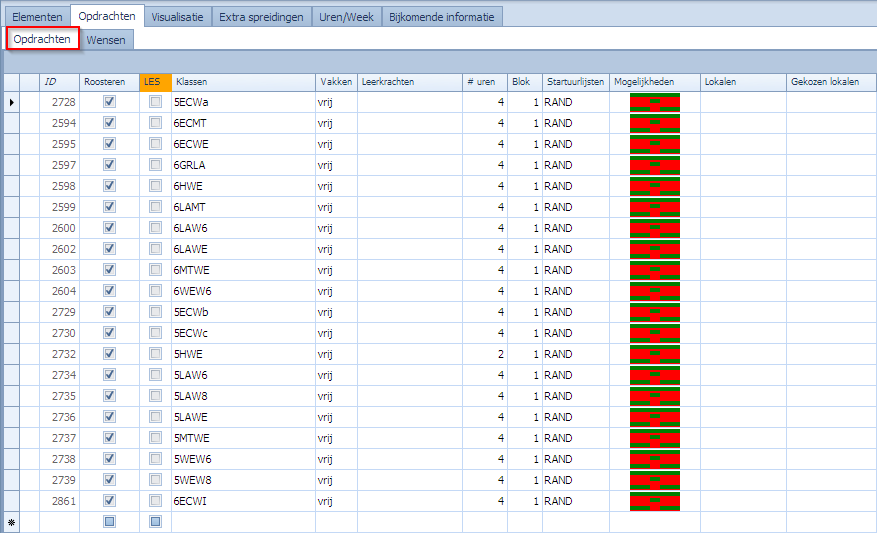
Als we het rooster nu zouden plannen, zonder verder beperkingen op de vrije uren dan komen er bijvoorbeeld volgende roosters uit:

Er ontstaan nu springuren (rood omkaderde vrije uren) die we niet wensen. We hebben extra beperkingen nodig om dit te vermijden. Een perfecte manier om dat te doen is via volgordespreidingen.

Een volgordespreiding werk steeds binnen een tijdsinterval dat via een uurlijst aan de spreiding gekoppeld wordt. De uurlijst bevat steeds het begin- en eindpunt van het tijdsinterval waarbinnen de controle moet gebeuren. Omdat we de vrije uren enkel toelaten op de randen (via uurlijst RAND) kunnen we de intervallen waarbinnen we de controle moeten doen ook beperken tot die randzone.

Bekijken we bijvoorbeeld de ochtendrand van vrijdag voor de klas 5ECWa [vr1,vr2]. Als we in dit interval via een volgordespreiding kunnen zeggen dat opdrachten met het vak “vrij” steeds vóór opdrachten met “LES” aangevinkt moeten liggen dan is het opgelost. Bekijken we de vrijdagavondrand voor 6HWE [vr8,vr9]. Als we hier met een volgordespreiding kunnen zeggen dat opdrachten met het val “vrij” ná opdrachten met “LES” aangevinkt moeten liggen dan is het ook daar opgelost.

Passen we dit systeem toe voor elke klas en rand dan is het opgelost. Eerst maken we een inventaris van de randen:

• BOVENRAND: “vrij” vóór “LES”: [ma1,ma2], [di1,di2], [wo1,wo2], [do1,do2], [vr1,vr2]
• ONDERRAND: “vrij” ná “LES”: [ma8,ma9], [di8,di9], [wo4,wo5], [do8,do9], [vr8,vr9]

Voor deze randintervallen maken we de nodige uurlijsten aan:

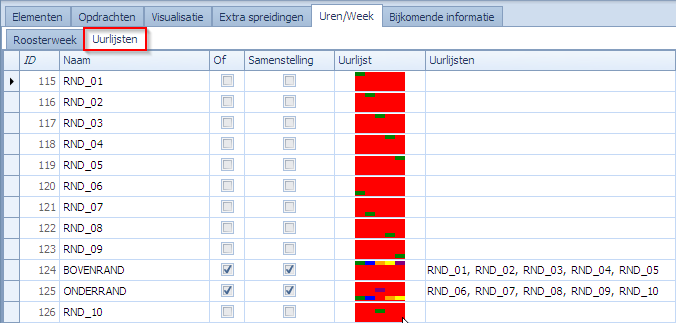
BOVENRAND groepeert de intervallen waar “vrij” vóór “LES” valt en ONDERRAND waar het “vrij” ná “LES” valt.

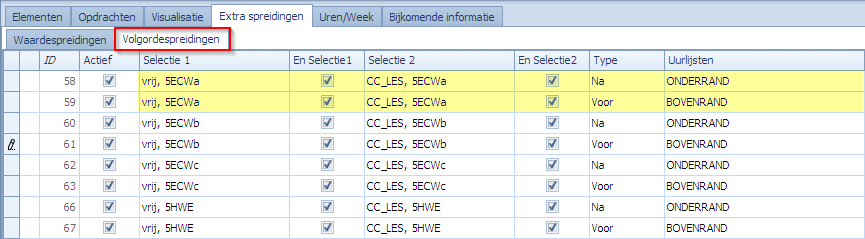
Per klas gaan we dan 2 volgordespreidingen moeten aanmaken. Bijvoorbeeld voor 5ECWa:

Volgordespreiding op de ONDERRAND:

• Controle wordt gedaan voor elk interval opgesomd in ONDERRAND (OF-uurlijst van koppels uren)
• Selectie 1: een EN-selectie die de criteria “5ECWa” en “vrij” combineert om alle opdrachten te nemen die vrije uren voor 5ECWa plaatsen.
• Selectie 2: een EN-selectie die de criteria “5ECWa” en custom kolom “LES” (vlagje aangevinkt) combineert om alle lesopdrachten voor 5ECWa te nemen.
• Type: “Na”. Dit wil zeggen dat de opdrachten uit Selectie 1 steeds ná die van Selectie 2 moeten komen binnen elk interval dat vervat zit in ONDERRAND.

Zelfde redenering voor BOVENRAND.

Merk op dat we dergelijke spreidingen per klas moeten neerschrijven. Momenteel bestaat er in Mondriaan geen kortere schijfwijze om dit te doen.

Dit lost dan het probleem op en zullen de vrije uren precies geplaatst worden zoals gevraagd.

Merk op dat het kan voorkomen dat alle randuren op woensdag vallen en dat er op woensdag dan maar 1 uur les gegeven zou worden. Wil men dit vermijden dan zou men nog een eenvoudige waardespreiding kunnen toevoegen die stelt dat elke klas op woensdag maximaal 2 vrije uren mag hebben.

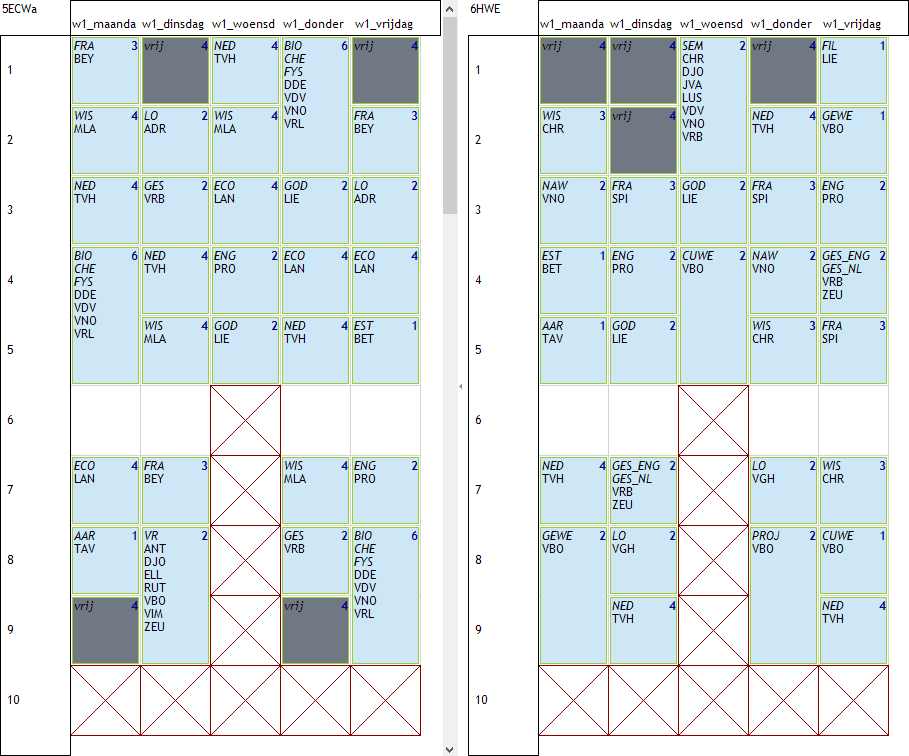
Voorbeeld van een oplossing:

Alternatief: Boven of onder maar niet beide

Indien men niet graag heeft dat klassen op dezelfde dag later beginnen en vroeger stoppen dan is daar ook een oplossing voor. Een klas mag ofwel later beginnen, ofwel vroeger stoppen. We laten alles hetzelfde als in de vorige oplossing maar de volgordespreidingen schrijven we nu als volgt:

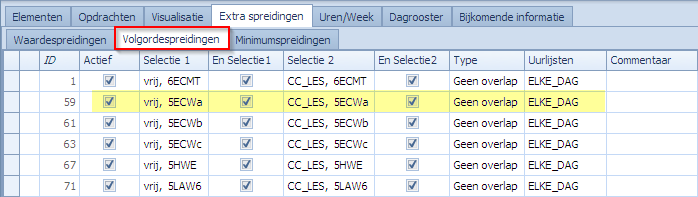
Waarbij ELKE_DAG een OF-uurlijst is van de 5 weekdagen.

Volgordespreiding op ELKE_DAG:

• Controle wordt gedaan voor elk dag opgesomd in ELKE_DAG (OF-uurlijst van koppels uren)
• Selectie 1: een EN-selectie die de criteria “5ECWa” en “vrij” combineert om alle opdrachten te nemen die vrije uren voor 5ECWa plaatsen.
• Selectie 2: een EN-selectie die de criteria “5ECWa” en custom kolom “LES” (vlagje aangevinkt) combineert om alle lesopdrachten voor 5ECWa te nemen.
• Type: “Geen overlap“. Dit wil zeggen dat alle opdrachten uit Selectie 1 ofwel voor ofwel ná die van Selectie 2 moeten komen op elke dag. Resultaat is dat de de vrije uren ofwel allemaal onderaan, ofwel allemaal bovenaan op een dag liggen.

Voorbeeld van een oplossing:

---

De uitgewerkte voorbeelden

Om de bestanden te gebruiken download men de zipfile en pakt men het bestand uit. Elke zipfile bevat 1 zttxml-bestand.

• U33 op 35 – Randuren boven – Enkel waardespreidingen
• U33 op 35 – Randuren boven – Blokjes met waardespreiding
• U33 op 41 – Randuren boven en onder – Blokjes met volgordespreiding
• U33 op 41 – Randuren boven of onder – Blokjes met volgordespreiding

(PS. Deze bestanden zijn te gebruiken vanaf Mondriaan versie 2020.2.0)