Opdrachten beperken door waardespreidingen
Inhoud
- Inleiding
- De essentie van de waardespreiding
- Mechanisme achter de waardespreidingen in detail
- Mogelijkheden om in één lijn verschillende waardespreidingen te definiëren
- Selectiecriteria in “Spreiding van…” via “Som” combineren in één waardespreiding
- Extra selectiecriteria in “Extra resources/selectiecriteria” via “En” combineren
- Eenvoudige waardespreidingen in het tablad “Opdrachten | Opdrachten”
- Waardespreidingen in combinatie met Partities van klassen
- Nog enkele tips
Inleiding
Opdrachten worden in hun mogelijkheden beperkt door volgende statische beperkingen:
- Mogelijke startpunten van de blokken/uren die geplaatst moeten worden
- Inherente beperkingen die aan de individuele resources van de opdracht opgelegd worden. Een leerkracht kan bijvoorbeeld niet op dinsdag aanwezig zijn.
Naast statische beperkingen zijn er dynamische beperkingen die de opdracht ondervindt tijdens het roosteren:
- Onbeschikbaarheid van resources op bepaalde momenten omdat andere opdrachten die resources al geplaatst hebben op die momenten.
- Eventueel beperkingen opgelegd door een venster waar de opdracht in geplaatst moet worden. Andere factoren kunnen de locatie van dat venster beperken.
- Eventueel beperkingen opgelegd door een “zelfde roosterpunt link” (ZR-Link) waarbij de plaats mee bepaald kan worden door andere opdrachten die in diezelfde roosterpunt link participeren.
Zowel deze statische als dynamische beperkingen zijn gebaseerd op de beschikbaarheid van resources op roosterpunten. Door in opdrachten resources samen te zetten moet automatisch aan een aantal voorwaarden voldaan worden opdat zulk een opdracht op een bepaald roosterpunt geplaatst kan worden.
Roosters die gemaakt worden op basis van dergelijke opdrachten garanderen dat er geen dubbele bezetting is van resources en garanderen eventueel nog enkele andere beperkingen zoals het samen in een een venster zitten van opdrachten of op het zelfde moment vallen in het rooster via een ZR-link.
Deze resourcebeperkingen (en startuurlijstbeperkingen) zijn vaak niet voldoende om de roosters te bekomen die men wenst. Een eenvoudig didactisch voorbeeld is het spreiden van een vak voor een klas. Heeft een klas 8 uur wiskunde dan is het volgens de resourcebeperkingen perfect in orde om deze 8 uur allemaal op dezelfde dag te organiseren. Dit is echter didactisch niet te verkiezen. Men wil bijvoorbeeld bekomen dat er maximum 2 uur per dag wiskunde gegeven wordt. Als men geen andere manier heeft om deze beperking uit te drukken zou men bijvoorbeeld het volgende kunnen doen:
- Maak 4 opdrachten die elk 2 uur plaatsen op willekeurige uren van een specifieke dag. Hier ontneem je dan de mogelijkheid waarbij er 3 dagen zouden zijn van 2 uur en 2 dagen van 1 uur. Door deze constructie verwijder je a priori een aantal mogelijkheden.
- Maak 1 opdracht die 8 uur plaatst op 10 mogelijke uren (bv ma1, di1, wo1, do1, vr1, ma2, di2, wo2, do2, vr2). Op deze manier laat je inderdaad toe dat er ofwel 4 dagen van 2 uur zijn, ofwel 3 dagen van 2 uur en 2 dagen van 1 uur. Het nadeel van deze oplossing is dat je de momenten in de dag erg beperkt. In dit voorbeeld laat je enkel het eerste en tweede uur van de dagen toe. In deze oplossing kan je er niet méér toelaten, want dan laat je de mogelijkheid toe dat er meer dan 3 uur op dezelfde dag vallen.
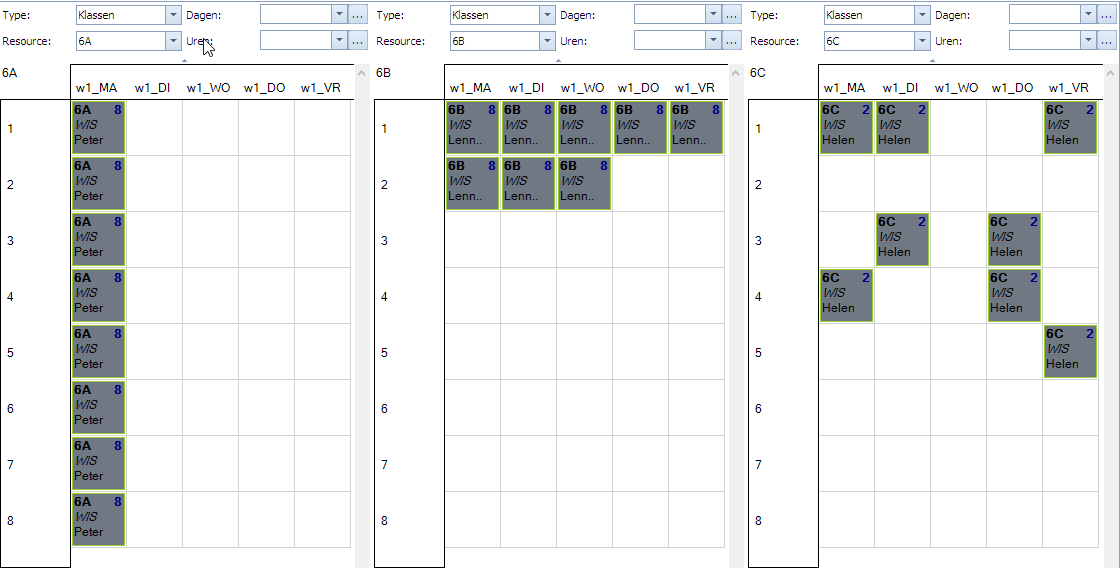
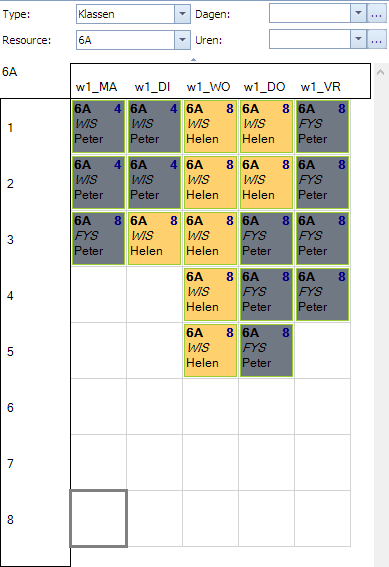
In volgend plaatje zien we 3 klassen (6A, 6B, 6C) waarvoor we telkens een ander soort opdracht gemaakt hebben voor 8 uur wiskunde:
- 6A: 8 uur zonder beperkingen: Mondriaan legt ze hier allemaal op maandag omdat er geen andere beperkingen zijn.
- 6B: 8 uur op een uurlijst van 10 uur (1ste en 2de uur van elke dag): Mondriaan kiest hier 3 dagen van 2 uur en 2 dagen van 1 uur.
- 6C: 4 opdrachten van 2 uur (woensdag uitgesloten): Mondriaan kiest voor elke opdracht individueel waar de 2 uren staan op de respectievelijke dag.
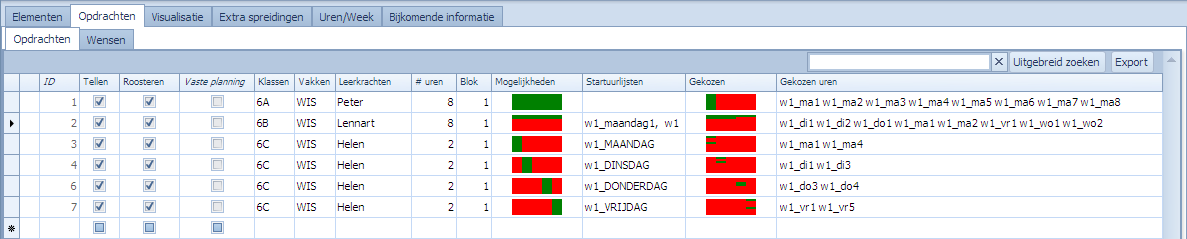
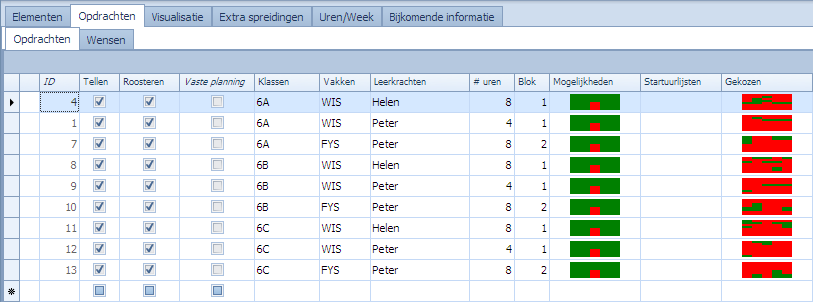
De opdrachten die aangemaakt werden voor dit eenvoudige voorbeeld zijn de volgende:
Via resourcebeperkingen en uurlijstbeperkingen kunnen we dit probleem dus niet algemeen oplossen. In elk van de voorgestelde oplossingen schrappen we mogelijkheden die we niet willen en ook niet hoeven te schrappen.
Om dit op te lossen hebben we een nieuw soort beperking nodig die iets overkoepelends zegt over een specifieke set van (deel)opdrachten. Wat we voor het voorbeeld willen kunnen zeggen is:
- Laat voor deze klassen maximum 2 uur wiskunde toe per dag van de week.
We beginnen met de opdrachten opnieuw te schrijven zoals ze bedoeld zijn: 8 uur wiskunde voor elke van de 3 klassen:
Vervolgens maken we in het tabblad “Extra Spreidingen | Waardespreidingen” één regel aan waarin we zeggen dat het voorkomen van wiskunde voor elk van de 3 klassen maximum 2 mag zijn per dag in de week.
Wat we uitdrukken met deze waardespreiding is het volgende:
- Neem alle opdrachten waar WIS in voorkomt.
- Verdeel deze set van opdrachten in 3 subsets van (deel)opdrachten:
- subset waar 6A in voorkomt
- subset waar 6B in voorkomt
- subset waar 6C in voorkomt
- Elk van deze subsets bestaat nu uit 8 deelopdrachten die elk 1 uur WIS moeten plaatsen.
- Voor elk van deze subsets zeggen we dat ze samen niet meer dan 2 uur mogen plaatsen op elke deeluurlijst die we in “Weekdagen” vinden.
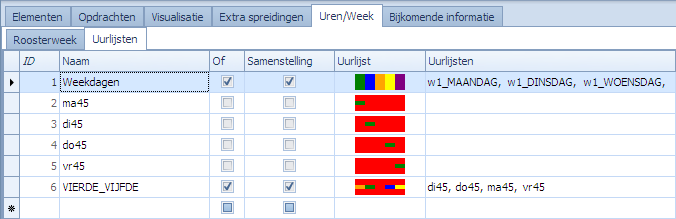
- Weekdagen is gedefinieerd in “Uren/Week | Uurlijsten” als een OF-constructie van 5 deeluurlijsten.
- Elk van die deeluurlijsten stelt een dag van 8 uur voor (w1_MAANDAG, w1_DINSDAG, …, w1_VRIJDAG)
Tijdens het roosteren gaat Mondriaan garanderen dat elk van die subsets van 8 deelopdrachten samen niet meer dan 2 uur kan plaatsen op elk van de vernoemde dagen.
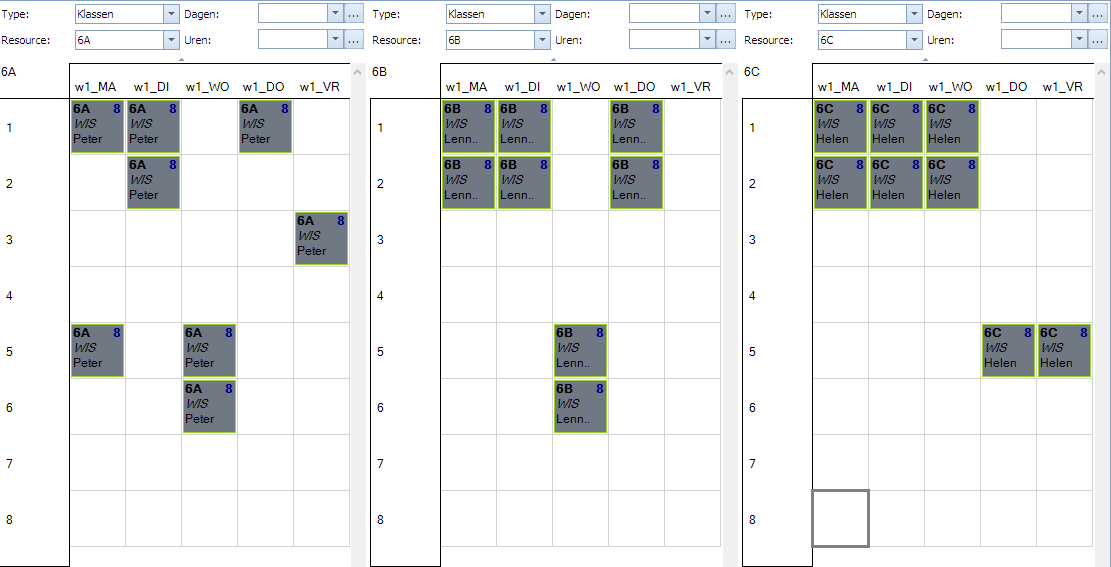
Laten we Mondriaan rekenen in de context van enkele andere beperkingen dan zou dit voor de 3 klassen een mogelijke oplossing kunnen zijn:
Voor elke klas hebben we nu een oplossing die voldoet aan de eis en waarvoor we niets in de opdrachten zelf hebben moeten aanpassen. Via waardespreidingen die los van de opdrachten gedefinieerd werden, hebben we exact die beperking kunnen opleggen die we wensten en dit zonder in te boeten op mogelijke oplossingen.
PS. Het voorbeeld dat we hier bekeken is zeer eenvoudig en meer nog, in het Opdrachten tabblad hebben we een manier voorzien om deze typische vakspreidingen meteen in de opdracht zelf op te nemen. Hierover volgt later meer.
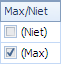
PS. Vanaf versie 2020.4.0 werd de kolom “Max” hernoemd naar “Max/Niet” omdat dit in feite de 2 opties zijn waaruit men kan kiezen. Ook de inhoud van de cellen van deze kolom ziet er iets anders uit. Als “Max/Niet” aangevinkt is ziet met “(Max)” naast de checkbox. In het andere geval ziet men “(Min)” naast de checkbox. Omdat er functioneel geen enkele wijziging is hebben we de screenshots op deze pagina hier niet aan aangepast. Vanaf versie 2020.4.0 ziet de inhoud van de cellen er dus als volgt uit:
De essentie van de waardespreiding
Een waardespreiding is een zeer eenvoudig concept. In de basis is het als volgt uit te leggen:
- van een welbepaalde set van opdrachten, door de gebruiker te bepalen
- telt men op elk moment het aantal uren (roosterpunten) dat ze bezet hebben in het rooster
- waarbij uren enkel geteld worden indien die uren op welbepaalde, door de gebruiker te bepalen, roosterpunten vallen
- en waarbij het gewicht van de opdrachten in de telling eventueel kan verschillen van opdracht tot opdracht
Vervolgens legt men een eis op aan de waarde van deze telling (gewogen som). Er zijn 2 soorten eisen die men kan opleggen:
- ofwel mag een bepaald maximum X niet overschreden worden
- ofwel mag de telling nooit een bepaalde waarde X hebben maar mag ze wel groter of kleiner zijn
Tijdens het roosteren (er wordt een oplossing gezocht door de engine van Mondriaan) worden alle waardespreidingen permanent geëvalueerd. Van zodra het plaatsen van een opdracht een waardespreiding zou schenden moet de engine een andere oplossing kiezen.
De complexiteit van waardespreidingen in het tabblad “Extra Spreidingen | Waardespreidingen” zit voornamelijk in volgende aspecten:
- Om het voor de gebruiker handiger te maken kan men patronen van waardespreidingen opgeven in één enkele regel in Mondriaan. Een voorbeeldje hiervan hebben we al laten zien in het WIS voorbeeld voor 6A, 6B, 6C. In feite hebben we hier in één regel 15 waardespreidingen beschreven:
- Voor 3 subsets aan opdrachten (voor elke klas in feite 8 deelopdrachten van 1 uur)
- Voor 5 dagen (telling moet gebeuren per dag van de week)
- Dat geeft dus 3 x 5 = 15 tellingen die moeten bekeken worden.
- Voor complexere eisen is het soms nuttig om binnen de set van opdrachten in de waardespreiding de ene opdracht een groter gewicht te geven in de telling dan een andere opdracht. De manier waarop die gewichten aangegeven worden kunnen vrij complex lijken.
Een eenvoudig voorbeeld van een waardespreiding met gewichten:
- Een klas heeft WIS en FYS als vakken en je hebt van elk vak bijvoorbeeld 8 uur die overal mogen staan in de week. Om de een of andere reden wil je eisen dat op woensdag het 1ste en 2de uur volgende regel geldt: WIS en FYS mogen elkaar niet opvolgen (naast elkaar liggen) op die 2 uren van woensdag.
- Deze eis kan je opleggen door één waardespreiding te definiëren waarbij je alle FYS en WIS opdrachten betrekt voor die klas.
- Aan de opdrachten met WIS geef je dan gewicht 1 en aan de opdrachten met FYS geef je gewicht 2.
- Als interval waarin geteld mag worden geef je wo1, wo2 op.
- Je stelt dat de som niet gelijk aan 3 mag zijn.
- Deze waardespreiding gaat dan toelaten dat 2 uur WIS elkaar opvolgen (som = 2), dat 2 uur FYS elkaar opvolgen (som = 4), dat er enkel 1 uur WIS staat (som = 1), dat er enkel 1 uur FYS staat (som = 2), dat er geen FYS en geen WIS staat (som = 0). Wat ze niet zal toelaten is dat er WIS naast FYS staan omdat de som daar dan 3 is.
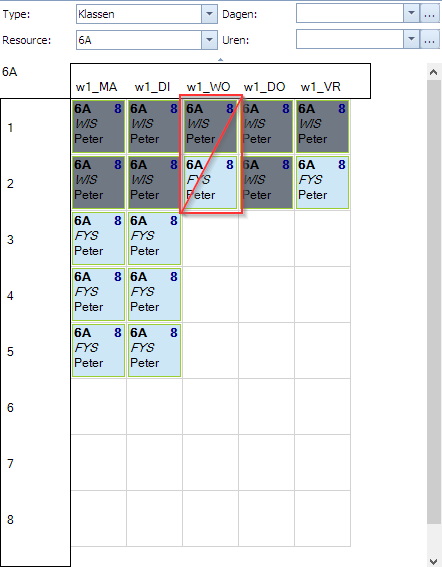
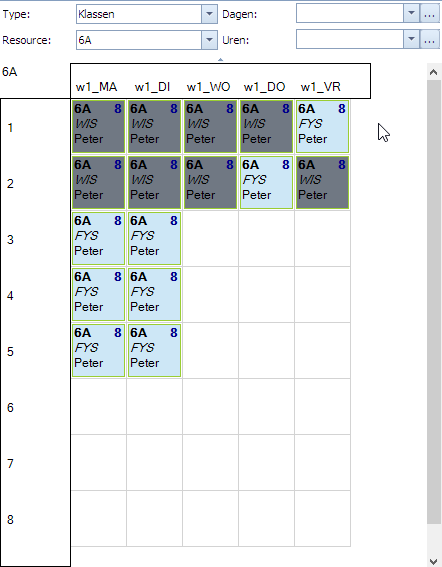
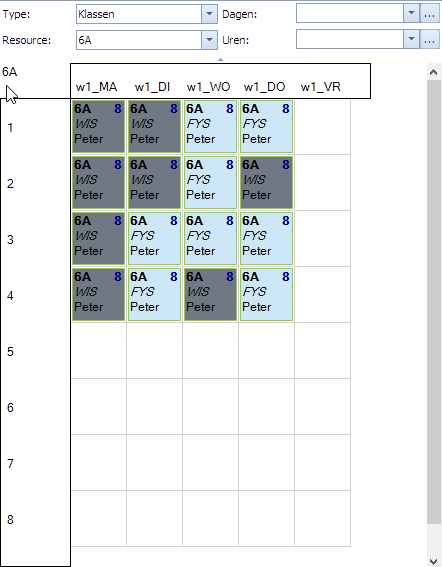
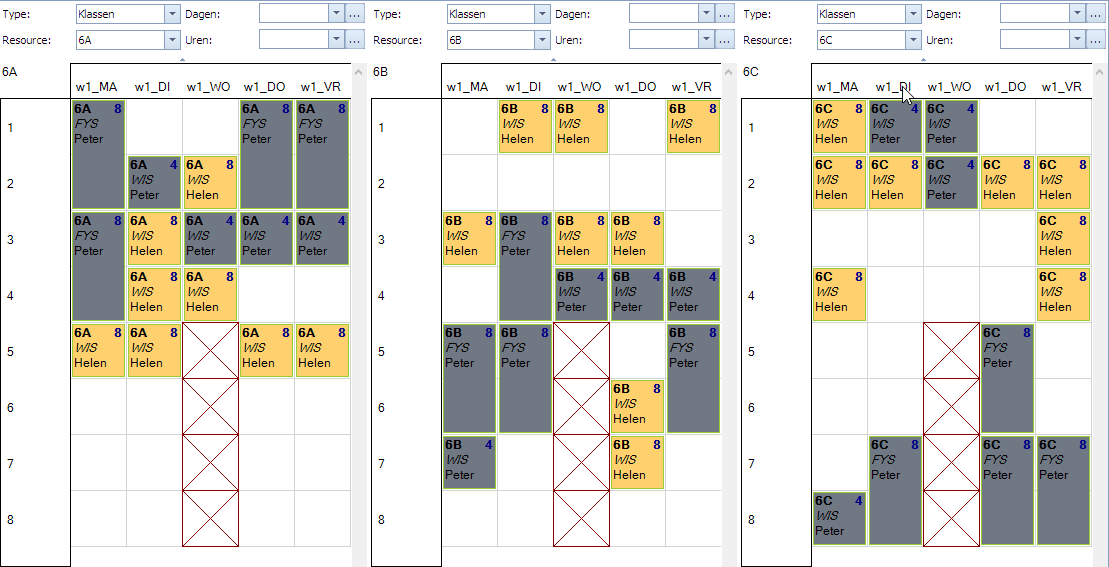
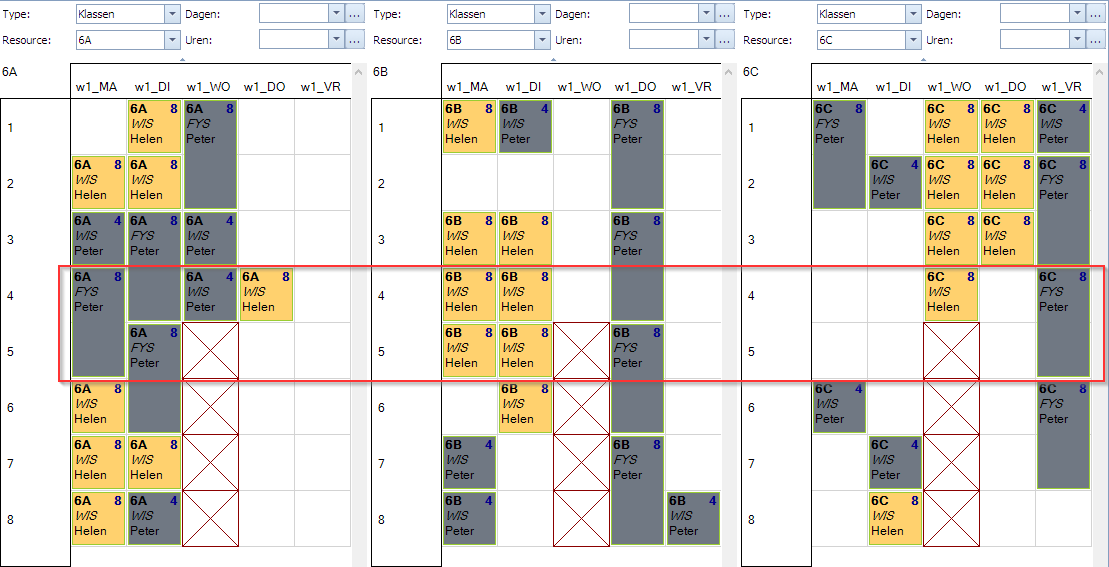
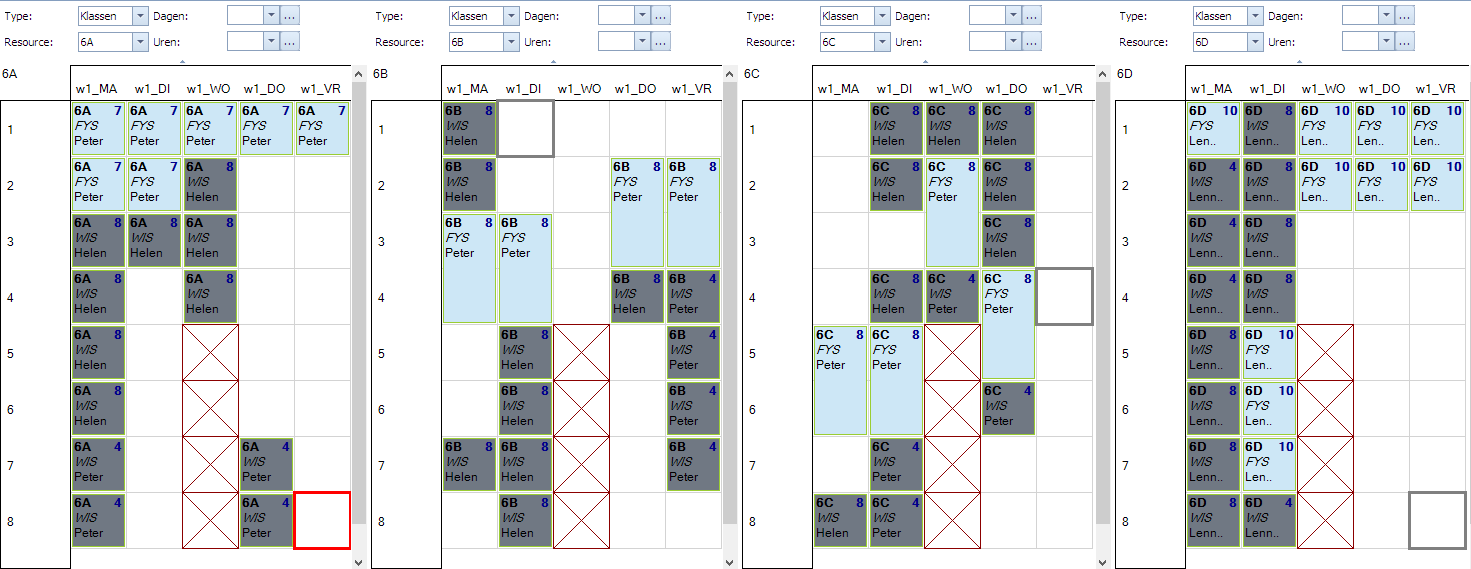
In volgend plaatje zien we links de situatie die we willen vermijden. WIS en FYS voor 6A mogen niet naast elkaar liggen op wo1,wo2. Het rechtse plaatje stelt bijvoorbeeld wel een toegestane situatie voor.
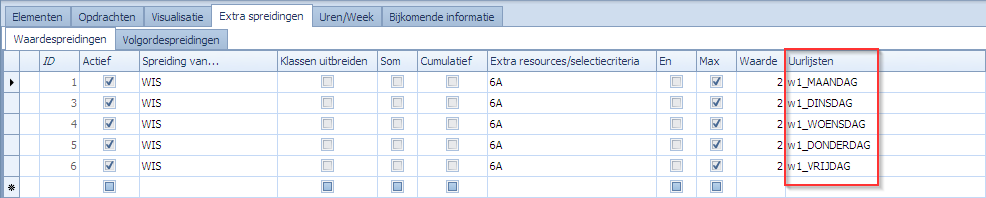
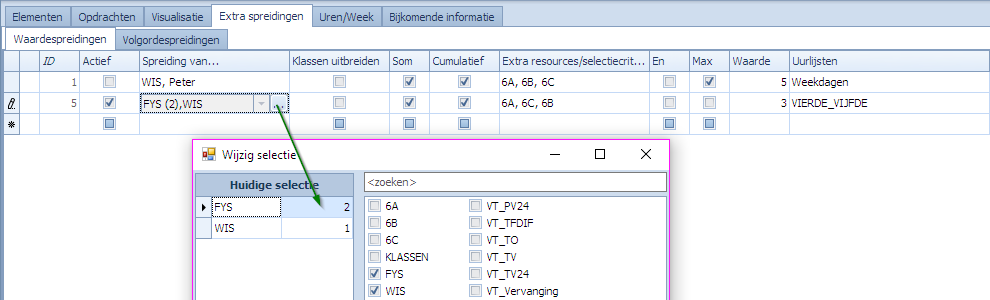
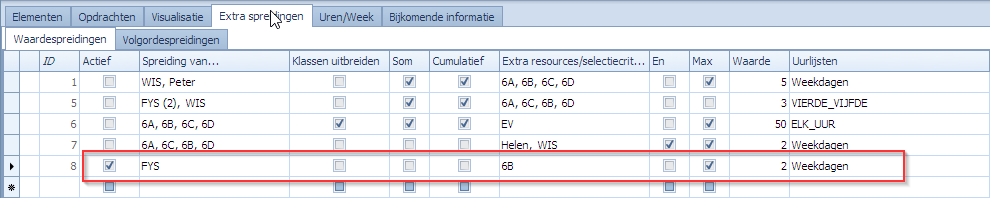
De waardespreiding om dit af te dwingen staat in de tweede lijn in dit scherm.
Wat betekenen de elementen in deze tweede waardespreiding?
Eerst kijken we naar de set(s) van opdrachten die geselecteerd worden door de waardespreiding. De kolom “Spreiding van …” bevat:
- set 1: WIS. Alle opdrachten waar WIS in voorkomt.
- set 2: FYS. Alle opdrachten waar FYS in voorkomt.
Deze 2 sets worden verder beperkt door wat in “Extra resources/selectiecriteria” staat. Voor beide sets houden we enkel die opdrachten over die ook 6A als resource bevatten. De kolom “Som” is aangevinkt. Dit wil zeggen dat set 1 en set 2 toch één waardespreiding vormen. Alle opdrachten van set 1 en set 2 worden samen geteld. Verder is ook de kolom “Cumulatief” aangevinkt. Dit wil zeggen dat het gewicht van een opdracht bepaald wordt door het aantal overeenkomstige selectiecriteria tussen wat in de kolom “Spreiding van …” staat en wat in de opdracht te vinden is. In ons geval hebben we ofwel WIS ofwel FYS maar niet beiden in dezelfde opdracht. Dus, dan blijft het gewicht 1. Echter, een extra aanduiding die we in “Spreiding van …” zien is een gewicht van 2 bij het vak FYS. Dit wil zeggen dat indien FYS voorkomt in de opdracht dat het gewicht van de opdracht cumulatief 2 toeneemt. In het voorbeeld gaan opdrachten met WIS dus voor 1 blijven tellen terwijl opdrachten met FYS voor 2 tellen en dat in dezelfde waardespreiding. Het gewicht van een opdracht in een spreiding wordt dus niet meer alleen bepaald door het aantal overeenkomtstige selectiecriteria maar ook door het gewicht van de criteria.
Tenslotte is de kolom “Max” uitgevinkt. Dat betekent dat het om een waardespreiding gaat waarbij de telling niet gelijk mag zijn aan de waarde 3 die in de kolom “Waarde” staat. De roosterpunten waarop de telling moet gebeuren is wo1, wo2.
Mechanisme achter de waardespreidingen in detail
Waardespreidingen worden door de gebruiker gedefinieerd in het tabblad “Extra spreidingen | Waardespreidingen”.
Een waardespreiding bestaat steeds uit volgende elementen:
- Een set van opdrachten die participeren in de telling.
- Per opdracht in de set een gewicht in de telling. Standaard is het gewicht 1.
- Een set van roosterpunten waarop de tellingen moet gebeuren.
Stel dat een opdracht een blok van 3 uur plaatst op wo1, wo2, wo3. Stel dat de set roosterpunten waarop geteld moet worden wo1, wo3, wo5 is. Stel dat het gewicht van de opdracht binnen de waardespreiding 2 is. Dan levert de telling voor deze opdracht 2*(1+1) = 4 op. Merk op dat het blok van 3 uur hier enkel 2 van de te bekijken roosterpunten bezet. Vandaar dat we 1+1 tellen. Het gewicht van de opdracht is 2, dat geeft 2*(1+1) = 4.
Volgende beschrijving geeft in detail weer hoe de telling gebeurt:
Mogelijkheden om in één lijn verschillende waardespreidingen te definiëren
Zoals eerder aangehaald zit de complexiteit van het maken van spreidingen onder andere in de interpretatie van de verkorte schrijfwijze van waardespreidingen. Er zijn namelijk verschillende manieren om verschillende waardespreidingen in één lijn te schrijven en de combinaties van die manieren maken het soms ingewikkeld om het te begrijpen. Als verschillende waardespreidingen in één lijn geschreven kunnen worden dan kunnen ze per definitie ook in verschillende lijnen geschreven worden. Andersom is het niet waar. Er zijn verschillende mogelijkheden om waardespreidingen te combineren in één lijn. We zullen via voorbeelden tot inzicht komen.
Waardespreidingen combineren op basis van de kolom “Uurlijsten”
Als je 2 of meerdere lijnen in het tabblad “Waardespreidingen” hebt die enkel verschillen in de Uurlijst die ze bevatten dan kan men ze groeperen door de uurlijsten te combineren in een OF-constructie. Merk op dat de uurlijst de roosterpunten voorstelt waarop de waardespreidingen hun tellingen moeten doen.
Voorbeeld: We hebben 5 lijnen met waardespreidingen waarbij het enige verschil de uurlijst is. Elk van deze waardespreidingen stelt dat WIS in 6A niet meer dan 2 uur op de roosterpunten van de uurlijst gegeven mag worden.
Een verkorte schrijfwijze voor deze 5 waardespreidingen is de volgende:
Belangrijk is dat de nieuwe uurlijst juist gedefinieerd wordt als een OF-constructie van die 5 oorspronkelijke dagen:
Waardespreidingen combineren op basis van de kolom “Extra resources/selectiecriteria”
Als 2 of meerdere lijnen in het tabblad “Waardespreidingen” enkel verschillen in de Extra resources/selectiecriteria die ze bevatten, dan kan men ze groeperen door de extra resources te combineren.
Voorbeeld: We hebben 3 lijnen met waardespreidingen waarbij het enige verschil de extra resources zijn. Elk van deze lijnen stelt dat WIS maar 2 uur gegeven mag worden op elke dag van de week voor hun respectievelijke klas.
Een verkorte schrijfwijze voor deze 3 lijnen is de volgende:
We zouden dit ook kunnen oplossen door een groep van klassen te definiëren en die te gebruiken in plaats van de individuele klassen te benoemen.
Omdat we in dit voorbeeld verder gebouwd hebben op het vorige voorbeeld, hebben we nu 3 x 5 = 15 waardespreidingen in één lijn geschreven.
Belangrijk: Dit is enkel geldig indien het vlagje “En” uitgevinkt staat in zowel de lange als de korte schrijfwijze. Zie verder voor de betekenis van dit vlagje.
Waardespreidingen combineren op basis van de kolom “Spreiding van …”
Als 2 of meerdere lijnen in het tabblad “Waardespreidingen” enkel verschillen in de “Spreiding van…” die ze bevatten, dan kan men ze groeperen door deze selectiecriteria te combineren.
Voorbeeld: We hebben 2 lijnen met waardespreidingen waarbij het enige verschil de “spreiding van…” criteria zijn. Elk van deze lijnen stelt dat een bepaald vak (WIS, FYS) maar 2 uur gegeven mag worden op elke dag van de week voor hun respectievelijke klas.
Een verkorte schrijfwijze voor deze 2 lijnen is de volgende:
We zouden dit ook kunnen oplossen door een groep van vakken te definiëren en die te gebruiken in plaats van de individuele vakken te benoemen.
Omdat we in dit voorbeeld verder gebouwd hebben op het vorige voorbeeld, hebben we nu 2 x 15 = 30 waardespreidingen in één lijn geschreven.
Belangrijk: Dit is enkel geldig indien het vlagje “Som” uitgevinkt staat (waardoor ook de kolommen “Cumulatief” en “Klassen uitbreiden” ook geen betekenis meer hebben) in zowel de lange als de korte schrijfwijze. Zie verder voor de betekenis van deze vlagjes.
Selectiecriteria in “Spreiding van…” via “Som” combineren in één waardespreiding
Tot nu toe hebben we enkel voorbeelden gezien waarbij de inhoud van “Spreiding van …” steeds tot meerdere sets leidt indien er meer dan één selectiecriteria in deze kolom staat. Staat er enkel WIS dan is WIS het enige selectiecriterium en is WIS niet verantwoordelijk voor de opdeling in meerdere waardespreidingen. Staat er WIS en FYS dan is dit een reden om de set aan opdrachten wel op de splitsen in verschillende sets die elk kunnen deel uitmaken van andere waardespreidingen. Dus, meerdere selectiecriteria hadden tot nu toe niet als gevolg dat er meer opdrachten in één waardespreiding konden komen.
Indien men de selectiecriteria in “Spreiding van …” wenst te gebruiken om één set aan opdrachten te selecteren dan moet men het vlagje “Som” aanvinken.
Voorbeeld: wenst men voor de klas 6A uit te drukken dat men nooit meer dan 4 uur WIS en FYS (gecombineerd) op een dag heeft kan men dat als volgt doen:
Door “Som” aan te vinken zegt men dat de selectiecriteria in “Spreiding van …” gecombineerd gebruikt mogen worden. De opdrachten die in dezelfde waardespreiding mogen participeren zijn nu opdrachten die WIS en/of FYS bevatten én die ook 6A bevatten.
Merk op dat deze lijn nu 5 waardespreidingen vertegenwoordigt, één per dag. Indien het vlagje “Som” niet aangevinkt zou zijn hebben ze 10 waardespreidingen. Volgend voorbeeld zou een mogelijk oplossing kunnen zijn die aan de gestelde eis voldoet. Op elke dag hebben we niet meer dan 4 uur van de vakken WIS en FYS samen.
Opmerking: indien er een andere, eenduidige eigenschap in de opdrachten zou zijn waarmee ze geselecteerd kunnen worden kan dat uiteraard ook zonder “Som” te gebruiken. Maar, van zodra “Som” gebruikt wordt zijn de criteria in “Spreiding van …” niet langer een aspect waarmee opdrachten in verschillende sets verdeeld worden.
Belangrijk i.v.m. gewichten: het aangevinkt zijn van “Som” heeft géén effect op het gewicht van de opdracht in de telling van de waardespreiding. Of een opdracht aan één of meerdere van de criteria voldoet heeft geen enkel effect op het gewicht. Elke opdracht heeft in dit geval een gewicht van 1. Het verhaal wordt anders indien de kolom “Cumulatief” aangevinkt wordt. Zie verder.
Indien “Som” aangevinkt is kunnen we nog steeds de waardespreidingen combineren in 1 lijn. Volgende 2 voorbeelden zijn dan ook equivalent:
In beide gevallen worden er hier 15 waardespreidingen gedefinieerd.
Gewicht van de opdrachten via “Cumulatief” laten afhangen van de selectiecriteria
Van zodra het vlagje “Som” aangevinkt is kan men ook het vlagje “Cumulatief” aanvinken. Door dit vlagje aan te vinken gaat het gewicht van een opdracht binnen de telling in de waardespreiding afhangen van:
- het aantal selectiecriteria uit de kolom “Spreiding van …” waaraan de opdracht voldoet. Heb je bijvoorbeeld in deze kolom FRA en HENJ staan dan zal een opdracht waarin alleen FRA staat of alleen HENJ staat een gewicht 1 krijgen maar de opdrachten waar zowel FRA als HENJ instaat het gewicht 2.
- optioneel rekening houdend met een extra multiplicator die op de selectiecriteria gedefinieerd is.
Voorbeeld 1: In 6A hebben we 12 uur WIS waarvan 4 gegeven door Peter en 8 door Helen. Verder geeft Peter nog 8 uur FYS in 6A en geen andere vakken. Nu willen we uitdrukken dat:
- 6A op dezelfde dag niet meer dan 5 uur WIS mag hebben
- 6A op dezelfde dag niet meer dan 5 uur les van Peter mag hebben
- Als Peter WIS geeft aan 6A dat dat dubbel telt omdat dat extra lastige lessen zijn
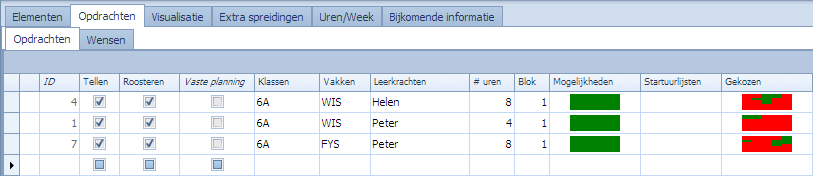
We hebben volgende eenvoudige opdrachten:
We maken een cumulatieve waardespreiding met volgende eigenschappen:
De waardespreiding moet op volgende manier geïnterpreteerd worden:
- selecteer alle opdrachten waar WIS en/of Peter in voorkomen. De “en/of” vanwege het vlagje “Som” dat aangevinkt is.
- geef de opdrachten waar enkel WIS zonder Peter en enkel Peter zonder WIS het gewicht 1
- geef de opdrachten waar WIS en Peter in voorkomen gewicht 2. Dit omdat het vlagje “Cumulatief” aangevinkt is.
- de telling moet op elke weekdag gebeuren en mag de waarde 5 niet overschreiden.
Het gaat in dit geval om 5 waardespreidingen, een per dag van de week.
Een mogelijke oplossing ziet er voor 6A als volgt uit:
Voorbeeld 2: We breiden dit voorbeeld verder uit door dezelfde opdrachten ook in 6B en 6C te geven door dezelfde leerkrachten. Ditmaal zorgen we er ook voor dat er op woensdagnamiddag geen les gegeven wordt in de 3 klassen, en dat het vak FYS in blokken van 2 uur gegeven wordt. Op deze manier kan men het samenspel tussen complexere waardespreidingen en resourcebezettingen in werking zien. Uiteraard zijn dit fictieve voorbeelden met enkel didactische waarde om de concepten uit te leggen.
De opdrachten zien er als volgt uit:
We maken een cumulatieve waardespreiding met volgende eigenschappen:
In plaats van enkel 6A staat er nu 6A, 6B, 6C in de “Extra resources/selectiecriteria”. Dit wil zeggen dat we nu 5 x 3 = 15 waardespreidingen hebben.
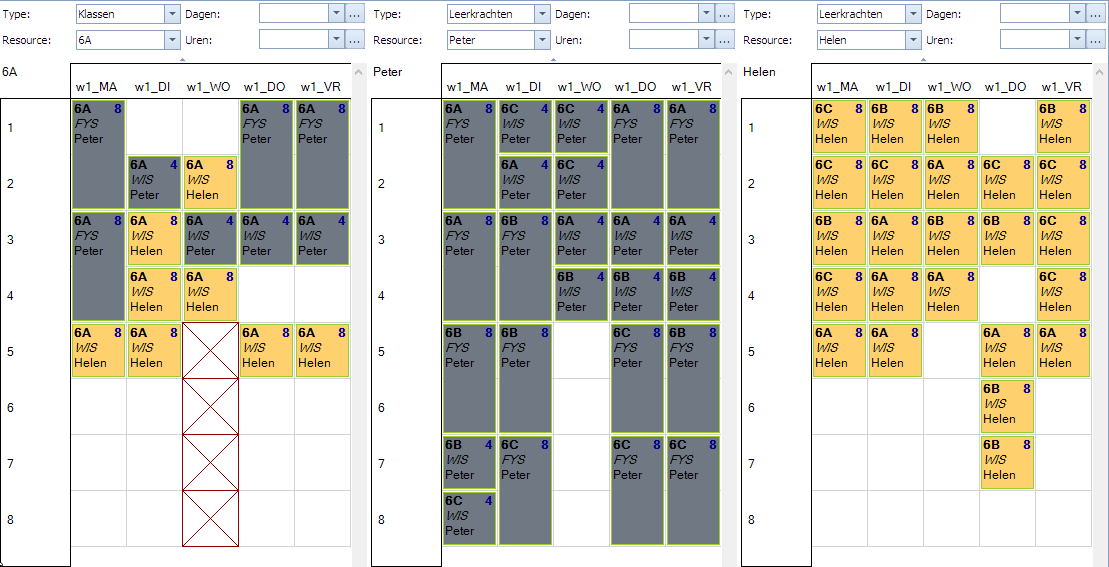
Een mogelijke oplossing voor deze 3 klassen ziet er als volgt uit en men kan voor elke dag en elke klas de proef op de som nemen. Elke dag klopt de telling. Nooit zal ze groter dan 5 zijn:
Zetten we in plaats van 6B en 6A de leerkrachten Peter en Helen in de roosters dan ziet men ook duidelijk wat de bezetting is van deze leerkrachten.
Voorbeeld 3: We hernemen de opdrachten van voorbeeld 2 en voegen een nieuwe eis toe die stelt dat op de overgang van het 4de naar het 5de uur geen overgang mag zijn van WIS naar FYS of van FYS naar WIS. Er mag op een 4de en 5de uur dus geen WIS en FYS naast elkaar te vinden zijn voor geen enkele klas.
De waardespreiding die we hiervoor kunnen opstellen zal als volgt werken:
- we geven het vak WIS een gewicht van 1
- we geven het vak FYS een gewicht van 2
- we hadden het evengoed andersom kunnen doen. Zolang er maar een van beide 1 heeft en de andere 2 als gewicht.
- we selecteren alle opdrachten waar FYS of WIS in voorkomen voor elke klas apart
- voor elk paar 4de en 5de uren en elke klas doen we de telling voor de geselecteerd opdrachten, rekening houdend met de gewichten
- we eisen dat die som nooit 3 kan zijn. Heb je 2 keer WIS dan is de som 2. Heb je 2 keer FYS dan is de som 4. Heb je enkel 1 uur WIS dan is de som 1. Heb je enkel FYS dan is de som 2. Heb je geen WIS en geen FYS dan is de som 0. Dus alles wat niet 3 is, is goed.
Om deze eis uit te kunnen drukken voorzien we de uurlijst VIERDE_VIJFDE die gedefinieerd wordt als een OF-lijst van 4 paren.
De waardespreidingen worden in de 2de lijn van dit scherm gedefinieerd. Via de elipsis (…) in “Spreiding van …” kan men de elementen selecteren en eventueel een gewicht meegeven. Voor ons voorbeeld geven we gewicht 2 aan FYS en het standaardgewicht 1 aan WIS. Van zodra men een gewicht groter dan 1 geeft ziet men het gewicht tussen haakjes staan in de kolom “Spreiding van …”. Verder zien we volgende parameters:
- “Som” aangevinkt: we willen dat de opdrachten met FYS en WIS samen geteld worden.
- “Cumulatief” aangevinkt: we willen dat opdrachten een gewicht krijgen in de telling. In dit geval wordt het gewicht mee bepaald door de gewichten bepaald in “Spreiding van …”
- “Extra resources/selectiecriteria”: We hebben 3 klassen als extra selectiecriterium. Voor elke klas willen we aparte waardespreidingen. Hiervoor moet “En” uitgevinkt staan.
- “En” uitgevinkt. (zie verdere voorbeelden van aangevinkt geval)
- “Max” uitgevinkt omdat we er een “Niet gelijk aan” waardespreiding van willen maken
- “Uurlijsten”: VIERDE_VIJFDE. Deze OF-uurlijst bevat 4 paren van 2 uur waarop geteld moet worden.
Hoeveel waardespreidingen worden er door deze 2 lijn gedefinieerd?
- 3 klassen x 4 uurlijsten = 12
Merk op dat we de eerste lijn uit voorbeeld 2 even op non-actief gezet hebben.
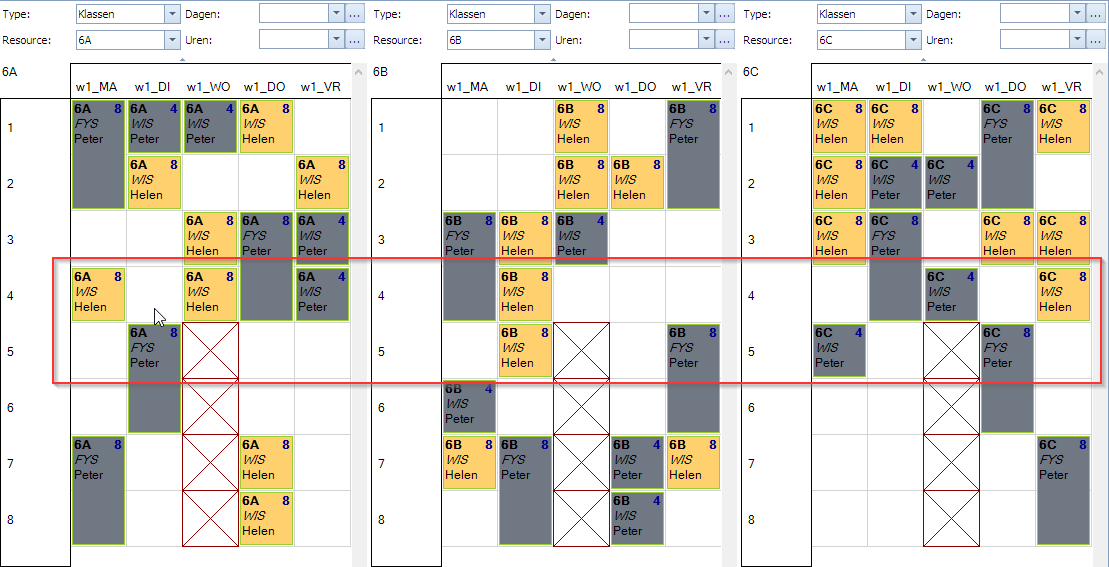
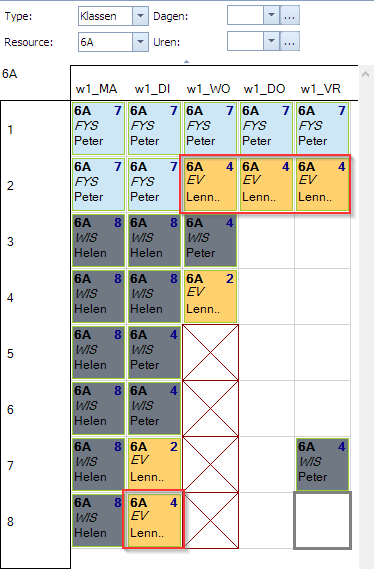
Volgend plaatje toont een mogelijke oplossing voor dit probleem. We gaan opnieuw uit van dezelfde opdrachten als in voorbeeld 2:
Het is duidelijk dat Mondriaan nu nergens op de overgang van het 4de naar het 5de uur wisselt tussen WIS en FYS. Dit kan men duidelijk zien in de rode kader.
Zetten we de waardespreidingen van zowel voorbeeld 2 als 3 actief dan hebben we 27 actieve waardespreidingen waar tegelijk aan voldaan moet worden.
Volgend plaatje troont een mogelijk oplossing die aan al deze voorwaarden voldoet:
Gewichten en eis te gebruiken als er meer dan 2 variabelen bekeken moeten worden
In het voorbeeld hebben we de gewichten 1 en 2 gebruikt voor WIS en FYS met de eis dat de som van de telling niet gelijk aan 3 mag zijn. Men kan dit systeem uitbreiden naar meerdere variabelen, waarbij het de bedoeling is dat één keer alle variabelen tellen in een waardespreiding niet toegelaten is. Volgend lijstje kan een leidraad geven:
- 2 Variabelen: Gewichten: 1, 2 – Eis: Niet 3
- 3 Variabelen: Gewichten: 1, 2, 4 – Eis: Niet 7
- 4 Variabelen: Gewichten: 1, 2, 4, 8 – Eis: Niet 15
- 5 Variabelen: Gewichten: 1, 2, 4, 8, 16 – Eis: Niet 31
- …
- n Variabelen: Gewichten: 1, 2, 4, …, 2^(n-1) – Eis: Niet 2^n – 1
Heeft men bijvoorbeeld 3 vakken (bv FRA, ENG, NED) voor een klas die onderling niet mogen wisselen op een urenpaar dan maakt men hier 3 waardespreidingen voor, telkens tussen 2 vakken. We reduceren dit probleem dan in feite weer naar 3 keer het probleem met 2 variabelen.
Deze techniek wordt bijvoorbeeld ook gebruikt om op bepaalde urenparen niet toe te laten dat een klas van locatie (gebouw) wisselt. Aan lokalen kan je een locatie koppelen. Ook deze locatie kan je gebruiken in “Spreiding van …”. Door de gewichten van de locaties goed te kiezen (bv 1 en 2) en een “Niet 3” eis kan men per klas en per urenpaar bepalen waar er niet gewisseld mag worden tussen lokalen.
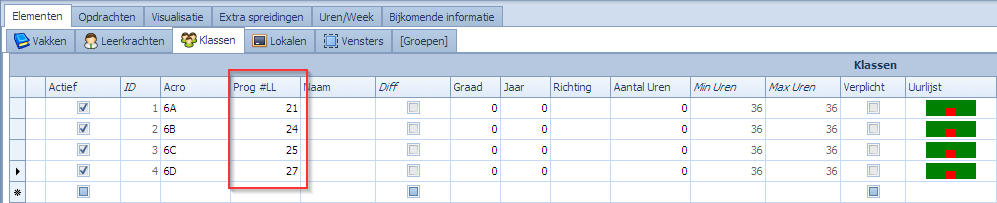
Voorbeeld 4: Een ander voorbeeld waar gewichten gebruikt kunnen worden is bij het roosteren van lessen/evenementen/refter waar bepaalde klassen samen komen op een plaats die een beperkte ruimte heeft. Je hebt bijvoorbeeld de mogelijkheid om 50 leerlingen tegelijk op die plaats te hebben maar je wenst niet op voorhand vast te leggen welke klassen samenzitten. Afhankelijk van de grootte van de klassen is een samenzetting al dan niet mogelijk. Stel dat we de klassen 6A, 6B, 6C, en 6D respectievelijk 21, 24, 25, en 27 leerlingen geven. Stel verder dat we per klas 16 uur in blokken van 4 het vak EV organiseren in een rooster dat verder al gevuld was door de opdrachten uit vorige voorbeelden. In het voorbeeld zullen we laten zien wat het effect is van geen waardespreiding te hebben en daarna een aantal gevallen waar we de limiet van 52 naar 51 en tenslotte naar max 50 leerlingen brengen.
We beginnen met voor de klassen het aantal leerlingen op te geven.
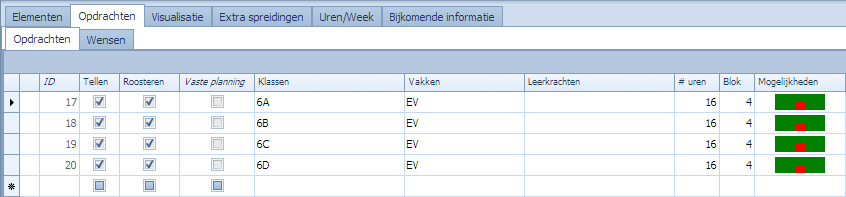
De specifieke EV opdrachten van 16 uur in blokken van 4 voeren we in in het opdrachten tabblad. Voor het gemak zonder leerkracht.
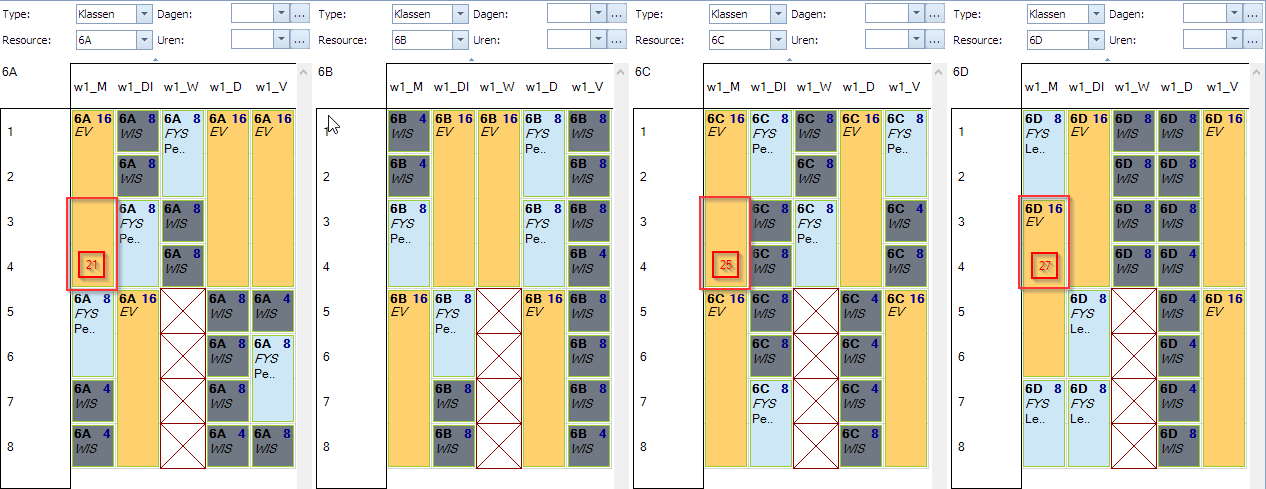
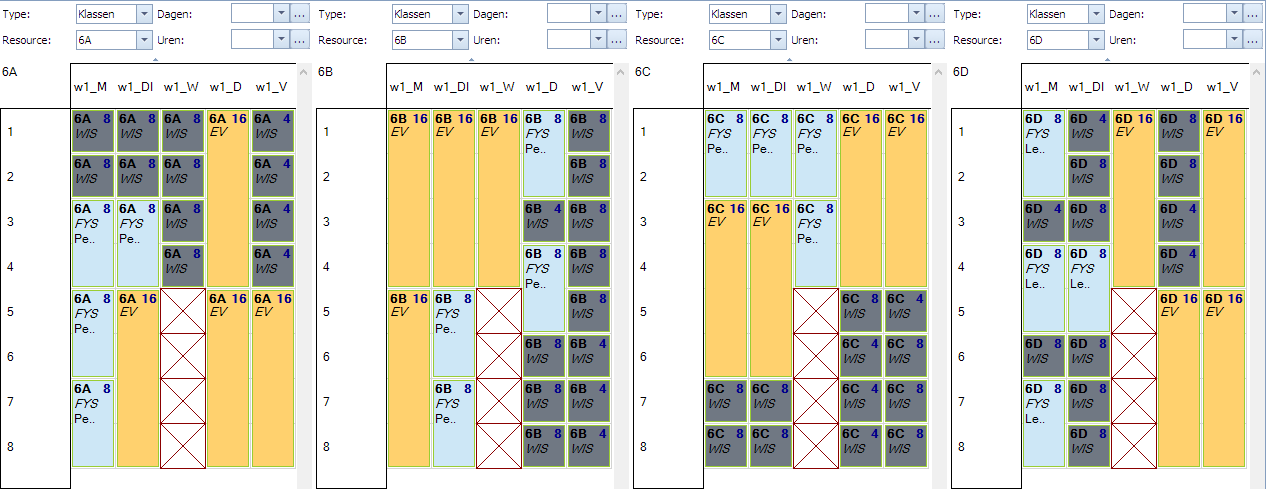
Zoeken we zonder waardespreiding een oplossing voor deze opdrachten dan zou dit er een mogelijke kunnen zijn. Merk op dat de geel/beige blokken de EV vakken voorstellen. Zonder enige waardespreiding kunnen die overal liggen. In dit voorbeeld zien we zelfs momenten waarop 3 klassen tegelijk EV hebben. Op ma3 en ma4 hebben 6A, 6C, en 6D samen het vak EV. Dat geeft samen 73 leerlingen wat veel te veel is. Vrijdagnamiddag heeft 6C en 6D samen EV. Dat is samen 52 wat ook nog teveel is. Door de juiste waardespreidingen kunnen we dit sturen.
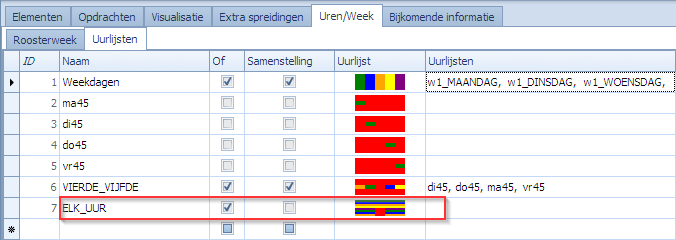
Om de waardespreidingen uit te kunnen drukken hebben we een uurlijst nodig van elk individueel uur. Op elk uur moet de telling kloppen over de klassen heen. We maken de OF-uurlijst “ELK_UUR” en nemen er elk uur in op. Neem je deze uurlijst op in een waardespreiding dan zal de telling op elk van de 36 uren apart gebeuren.
Als waardespreiding definiëren we de volgende lijn:
Elementen van de waardespreiding:
- We nemen 4 klassen op en “Spreiding van…”
- Het vlagje “Klassen uitbreiden” staat aangevinkt en betekent dat het gewicht van de respectievelijke klassen bepaald wordt door het aantal leerlingen dat in de klas gedefinieerd is. Dus, als je een opdracht in de telling hebt die 6A bevat, dan telt die opdracht voor 21 in de telling. Heb je een opdracht die een samenzetting heeft van 6A en 6B dan telt die opdracht voor 45 in de telling.
- Het vlagje “Som” staat aangevinkt en betekent dat alle opdrachten geselecteerd in “Spreiding van…” als één set aan de telling deelnemen. Er is geen opsplitsing per klas.
- Het vlagje “Cumulatief” staat aangevinkt wat betekent dat er met de gewichten rekening moet gehouden worden tijdens de telling. In dit geval gaat het dan om de gewichten beplaalt door het aantal leerlingen per klas.
- In “Extra resources/selectiecriteria…” hebben we het vak EV als selector toegevoegd. We mogen enkel opdrachten opnemen in de telling die te maken hebben met het vak waarvoor we de telling willen uitvoeren.
- Het vlagje “Max” staat aangevinkt wat betekent dat de telling een maximale waarde niet mag overschrijden.
- De “Waarde” zetten we op 60.
- In “Uurlijsten” zetten we de OF-uurlijst van 36 individuele uren.
Dit geeft een totaal van 36 waardespreidingen die tijdens het zoeken naar een oplossing gerespecteerd moeten worden.
Om het effect van het getal in “Waarde” te zien op het resultaat laten we dat variëren van 52, naar 51, naar 50.
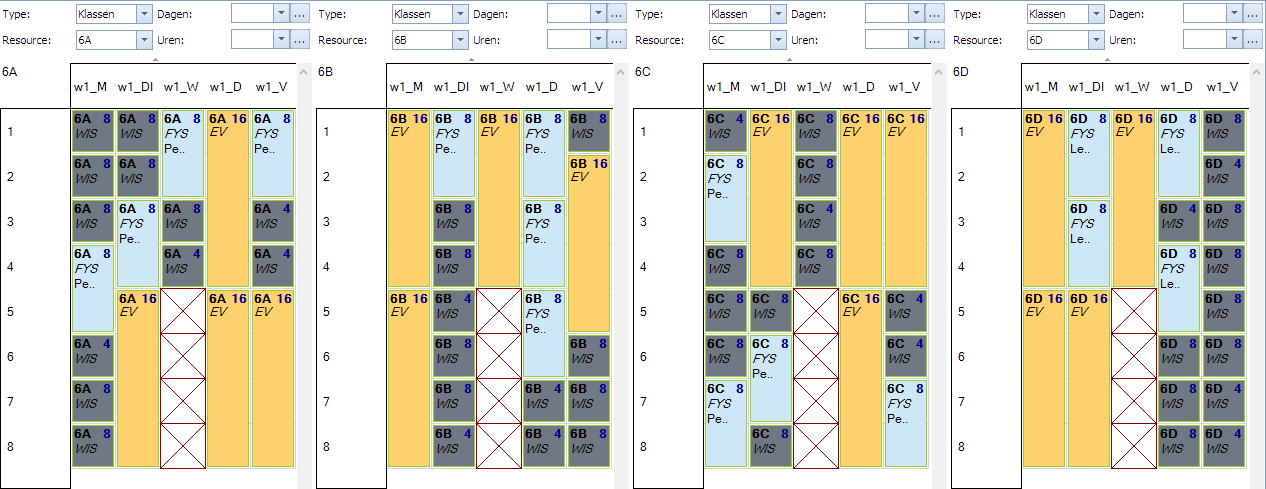
Max “Waarde” = 52
Hier zien we dat er nergens meer dan 2 klassen tegelijk EV kunnen hebben. Echter, elke combinatie van 2 klassen is nog mogelijk omdat geen enkele combinatie boven 52 kan komen. 3 klassen zie je nergens meer.
Max “Waarde” = 51
Hier is de eis al iets strenger en wat hier uitgesloten wordt is dat 6C en 6D nog samen kunnen zitten omdat dat samen 52 zou geven. Alle andere combinaties van 2 zijn nog toegelaten.
Max “Waarde” = 50
Hier is de eis nog strenger en zal ook 6D en 6B niet samen kunnen zitten. Men ziet duidelijk dat het systeem voor samenzettingen streeft naar 6D en 6A, wat samen 48 geeft en 6B en 6C wat samen 49 geeft.
Extra selectiecriteria in “Extra resources/selectiecriteria” via “En” combineren
De laatste optie die nog besproken moest worden is de optie “En” die effect heeft op selectie gemaakt via de kolom “Extra resources/selectiecriteria”. Normaal wordt de kolom “Extra resources/selectiecriteria” gebruikt om de opdrachten verder in sets uit te splitsen om er aparte waardespreidingen van te maken. In het geval dat het vlagje “En” aangevinkt is is het effect echter heel anders. Alle selectiecrietria vermeld in “Extra resources/selectiecriteria” moeten tegelijk aanwezig zijn in een opdracht opdat ze geselecteerd zou kunnen worden.
Voorbeeld: stel dat we voor elke klas apart willen bekomen dat indien Helen er WIS geeft dat ze dat dan maximum 2 uur per dag mogen hebben.
We voeren volgende lijn in om deze waardespreidingen te maken:
Elementen van de waardespreiding:
- We nemen 4 klassen op en “Spreiding van…”
- In “Extra resources/selectiecriteria…” hebben we het vak WIS en leerkracht Helen als selector toegevoegd.
- Het vlagje “En” is aangevinkt. Hiermee zeggen we dat enkel opdrachten die zowel Helen als WIS bevatten geselecteerd worden voor de waardespreiding.
- Het vlagje “Max” staat aangevinkt wat betekent dat de telling een maximale waarde niet mag overschrijden.
- De “Waarde” zetten we op 2.
- In “Uurlijsten” zetten we de OF-uurlijst 5 weekdagen.
Hoeveel waardespreidingen worden hier gedefinieerd:
- 4 klassen, per klas aparte waardespreidingen omdat “Som” niet aangevinkt is.
- Geen verdere opsplitsing via “Extra resources/selectiecriteria” omdat “En” aangevinkt is.
- 5 uurlijsten, één voor elke weekdag
Dat geeft samen 4×5 = 20 waardespreidingen.
Een mogelijke oplossing waarmee met de nieuwe eis rekening gehouden wordt is de volgende:
Merk op dat voor 6D geen lessen WIS met Helen ingericht werden. Voor de andere 3 klassen ziet men duidelijk dat er max 2 uur per dag gegeven worden van die specifieke lessen. We hebben de kleuring hier voor het gemak op leerkracht gedaan. Geel/Beige vlakken zijn allemaal lessen door Helen gegeven.
Eenvoudige waardespreidingen in het tablad “Opdrachten | Opdrachten”
Een erg veel voorkomende waardespreiding heeft te maken met de eenvoudige eis dat een vak goed gespreid moet zijn in de week. Heeft een klas het vak FRA 4 uur per week dan is het niet wenselijk dat dat bijvoorbeeld 3 uur op één dag gegeven wordt, of misschien zelfs niet eens 2 uur op één dag. Heeft men het vak WIS 7 uur per week dan zouden we bijvoorbeeld liefst zien dat dat vak op ten hoogste twee dagen 2 uur gegeven wordt en de andere dagen 1 uur. Allerlei variaties op dit thema zijn mogelijk.
Omdat dit vaak voorkomende spreidingseisen zijn heeft Mondriaan in het Opdrachten tabblad een mechanisme voorzien om dergelijke eenvoudige vakspreidingen automatisch aan te maken op basis van een aantal eenvoudige parameters:
- Spreiding: normaal te verwachten maximum aantal uren per dag van het vak in de opdrachtlijn.
- Uitz. dagen: aantal dagen waar we een uitzondering toelaten
- Uitz. uren: maximaal aantal uren op de uitzonderingsdagen
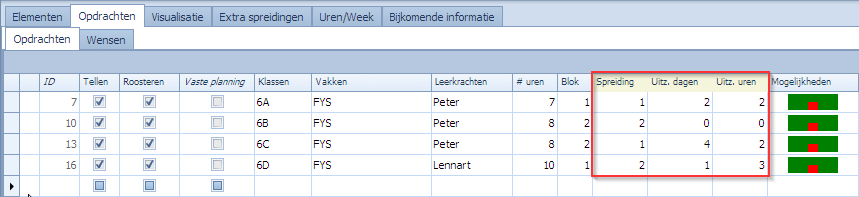
Enkele voorbeelden:
Voorbeelden uitgelegd:
- in 6A worden 7 losse uren FYS georganiseerd. Normaal laten we maximim 1 uur per dag toe maar omdat het 7 uur zijn lukt dat niet en laten we 2 uitzonderingsdagen toe waar max 2 uur gegeven worden.
- in 6B worden 4 blokken van 2 uur FYS georganiseerd. We laten maximum 2 uur per dag toe zonder verdere beperkingen.
- in 6C worden 4 blokken van 2 uur FYS georganiseerd. Normaal laten we 1 uur per dag toe (gaat niet met blokken van 2) en 4 uitzonderingsdagen van 2 uur (dat lost het dan op).
- in 6D worden 10 losse uren FYS georganiseerd. Normaal laten we 2 uur per dag toe wat zou moeten lukken. Echter, we staan 1 dag toe van 3 uur.
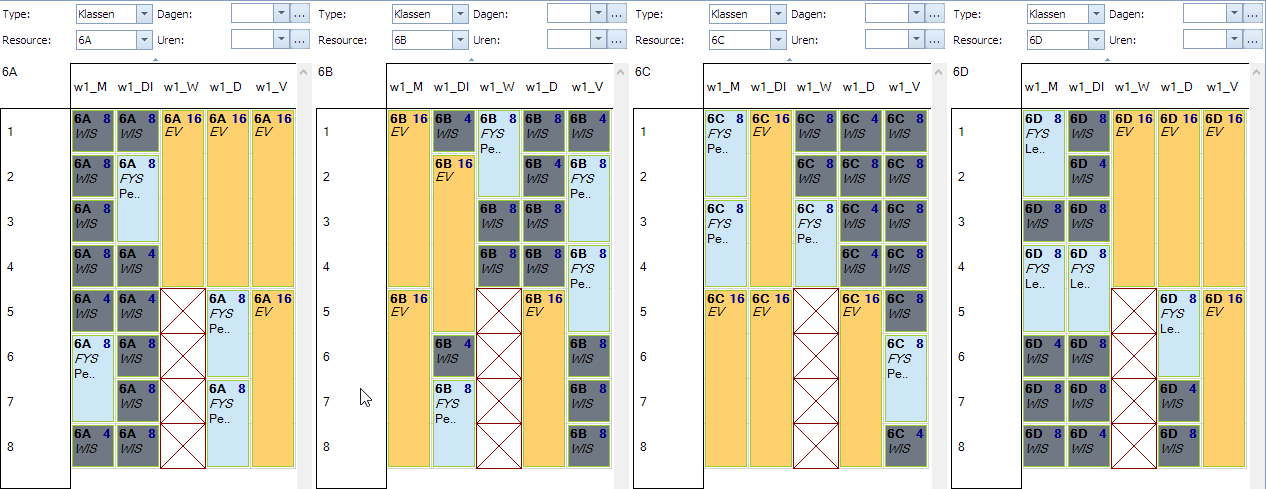
Een mogelijke oplossing van dit probleem zou de volgende kunnen zijn:
Achter de schermen maakt Mondriaan de nodige waardespreidingen aan om deze eisen af te dwingen. Deze waardespreidingen kan de gebruiker echter niet zien of aanpassen. Het is echter wel nuttig om te begrijpen hoe Mondriaan waardespreidingen maakt om aan deze eisen te voldoen. We nemen er 2 voorbeelden uit.
Voorbeeld 1: 6B mag maximum 2 uur FYS per dag hebben.
Hiermee selecteren we alle opdrachten waar FYS instaat en we vernauwen de set tot opdrachten waar ook 6B instaat.
Voorbeeld 2: 6A mag maximum 2 dagen hebben waar ze 2 uur FYS hebben, de andere dagen is het maximum 1 uur.
Dit is een complexer probleem. Om dit op te lossen met waardespreidingen kunnen we als volgt te werk gaan:
- Stel eerst dat er geen enkele dag mag zijn waarop er meer dan 2 uur FYS gegeven wordt.
- Dit belet niet dat er meer dan 2 dagen zijn waarop er 2 uur les gegeven wordt.
- Als men 3 willekeurige dagen uit de week bekijkt dan mogen er op die 3 dagen nooit meer dan 5 uur FYS gegeven worden. Doet men dit voor elke mogelijke combinatie van 3 dagen dan is het probleem opgelost.
Er zijn dus 2 soorten waardespreidingen nodig:
- max 2 uur FYS per dag en dat voor elke dag
- max 5 uur FYS per 3 dagen en dat voor elke combinatie van 3 dagen
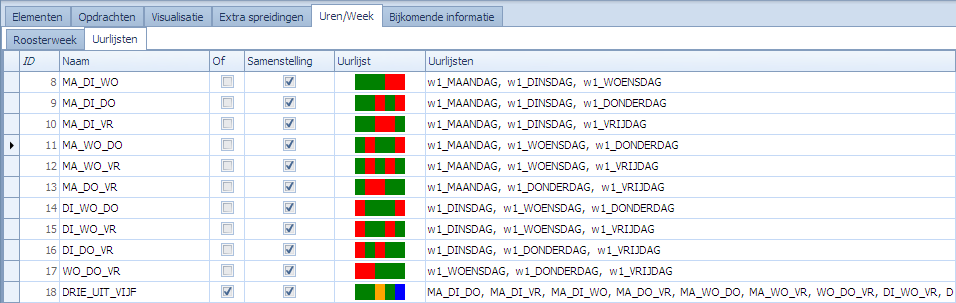
De complexiteit zit nu in die 2de waardespreiding. De uurlijst waarom we die 5 uur moeten controleren moet een OF-uurlijst zijn waarin elke combinatie van 3 dagen zit. Die uurlijst bouwen we als volgt op:
We hebben hier 10 combinaties van 3 dagen. Bijvoorbeeld MA_DI_WO is de samenvoeging van de uren van maandag, dinsdag, en woensdag. Na het maken van de 10 mogelijke combinaties van 3 dagen maken we een uurlijst die alles combineert: DRIE_UIT_VIJF. Dit is een OF-uurlijst die alle 10 de uurlijsten bevat.
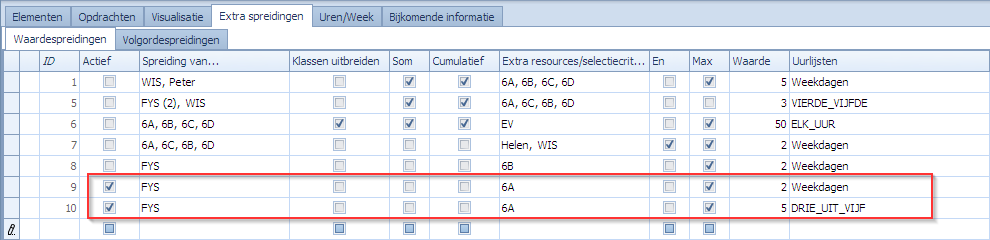
Als waardespreidingen definiëren we dan de volgende voor 6A:
Deze 2 lijnen geven hetzelfde resultaat als de vakspreiding die we voor 6A in het Opdrachten tabblad hadden voorzien.
Localiteit van de waardespreidingen in het Opdrachten tabblad
Er is een zéér belangrijke beperking voor waardespreidingen die via het Opdrachtentabblad ingevoerd worden. De waardespreiding is enkel en alleen van toepassing op de opdrachtlijn waarin ze gedefinieerd is. Dus, daar waar we in het tabblad “Extra spreidingen” zelf kunnen bepalen welke opdrachten er meespelen in de tellingen van de waardespreiding is dat niet het geval voor de eenvoudige vakspreidingen opgegeven via het Opdrachten tabblad. De opdrachten die meespelen in de telling van een waardespreiding zijn exact die opdrachten gedefinieerd in de opdrachtlijn waarin de vakspreiding staat.
Een voorbeeld maakt dit duidelijk. Stel dat we het vak EV 6 uur geven in 6A. Om een of andere reden wordt dit opgesplitst in 2 opdrachtlijnen in het Opdrachten tabblad. De eerste lijn bevat 4 uur, de tweede lijn nog eens 2 uur. Voor elk van de lijnen zeggen we dat er max 1 uur per dag gegeven mag worden:
Als we dit roosteren krijgen we volgende mogelijke oplossing:
Hier ziet men dat de vakspreiding gerespecteerd wordt voor de opdrachten waar ze voor gedefinieerd werden:
- de 4 deelopdrachten van de eerste lijn zijn onderling perfect gespreid (zie 4 rood omkaderde geel/beige opdrachten in het rooster)
- de 2 deelopdrachten van de tweede lijn zijn onderling perfect gespreid (zie 2 niet omkaderde geel/beige opdrachten in het rooster)
Tussen de opdrachten van de eerste en de tweede lijn is geen enkele relatie i.v.m. spreidingen te bespeuren. Wil men dat die relatie wel bestaat dan moet men:
- ofwel deze 6 uur in één opdrachtlijn definiëren en er een goede vakspreiding op plaatsen
- ofwel zelf de juiste waardespreidingen in het tabblad Extra spreidingen definiëren.
De vakspreidingen in het Opdrachten tabblad zijn dus steeds en enkel van toepassing op de opdracht waar ze bij staan in het Opdrachten tabblad. Dit is vaak een bron van verwarring.
Weekspreidingen in het opdrachtentabblad in een multiweeksysteem
(vanaf versie 2021.5.0)
Naast opdrachtspreidingen in het opdrachtentabblad (voor dagen binnen één week) bestaat er in een multiweeksysteem ook de mogelijkheid om weekspreidingen te definiëren voor de opdracht. De principes uitgelegd voor opdrachtspreidingen gelden ook voor de weekspreidingen. Ook voor weekspreidingen worden er achter de schermen waardespreidingen aangemaakt op basis van de opgegeven parameters:
- Weekspreiding: normaal te verwachten maximum aantal uren per week van het vak in de opdrachtlijn.
- Uitz. weken: aantal weken waarvoor we een uitzondering toelaten.
- Week Uitz. uren: toegelaten maximaal aantal uren per week voor de uitzonderingsweken.
Deze parameters kan men enkel opgeven indien de kolom Weken leeg is. Voor weekopdrachten heeft het geen zin om weekspreidingen te definiëren omdat men voor weekopdrachten per definitie aangeeft hoeveel uur er in elke week moet doorgaan.
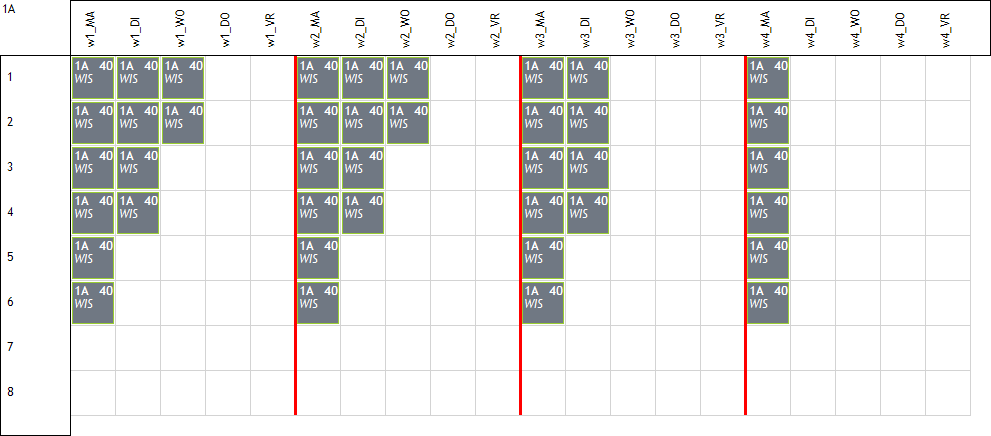
Voorbeeld: Kathleen geeft in een 4-weken systeem 40 uur wiskunde aan 1A. We eisen dat er normaal max 10 uur per week doorgaan maar voor 2 weken laten we een uitzondering van 12 uur toe. Merk op dat ook de normale opdrachtspreiding (Spreiding/Uit. dagen/Uitz. uren/Uitz. per week) blijft werken.

Het resultaat zou er als volgt kunnen uitzien:
Wat gezegd werd over de localiteit van de waardespreiding voor opdrachtspreidingen geldt ook voor deze weekspreidingen.
Waardespreidingen in combinatie met Partities van klassen
Spreidingen kan men niet specifiek voor partitie-elementen definiëren. Echter, als men spreidingen definieert voor klassen die op hun beurt in partities ingedeeld en geroosterd worden, dan moeten we wel degelijk naar het effect hiervan kijken.
Partities
Voor we de effecten beschrijven nog enkele feiten over partities op een rij:
- Een klas kan opgedeeld worden volgens verschillende criteria (partities). Voorbeelden hiervan zijn:
- Geslacht (meisje/jongen)
- Levensbeschouwing (RKG/NCZ/ISL/PGD)
- Optievak (Mechanica/Telecom)
- In het eerste voorbeeld is de partitie “Geslacht” en zijn de partitie-elementen “meisje” en “jongen”
- Een klas is steeds volledig opgedeeld volgens elke partitie. Dit wil zeggen dat elke leerling van de klas in principe voor elke Partitie een keuze moet maken voor een van de partitie-elementen.
- Partitie-elementen kunnen afzonderlijk geroosterd worden.
- Partitie-elementen van eenzelfde partitie kunnen op hetzelfde roosterpunt liggen maar dat hoeft niet.
- Partitie-elementen van verschillende partities kunnen NOOIT op hetzelfde roosterpunt liggen. Voorbeeld: moest het partitie-element “jongen” op hetzelfde roosterpunt liggen als “Mechanica” dan zou dit uitsluiten dat een jongen Mechanica kan volgen. Dat kan dus niet en Mondriaan zorgt ervoor dat dit gerespecteerd blijft.
Stel dat we een klas K hebben die volgens de partities Geslacht en Levensbeschouwing opgedeeld wordt. Omdat elke combinatie mogelijk is delen we K impliciet op in volgende 8 subklassen:
- meisje-RKG
- meisje-NCZ
- meisje-ISL
- meisje-PGD
- jongen-RKG
- jongen-NCZ
- jongen-ISL
- jongen-PGD
Elke leerling MOET in één van deze 8 subklassen zitten omdat hij een keuze gemaakt moet hebben voor elke partitie. De som van al deze subklassen is terug de volledige klas.
Enkele opdrachtvoorbeelden:
- Een opdracht die voor de volledige klas K 1 uur WIS plant: In feite plaatst die opdracht dan deze 8 subklassen op hetzelfde roosterpunt.
- Een opdracht die voor de meisjes 1 uur LO plant: In feite plaatst die opdracht dan 4 subklassen op hetzelfde roosterpunt: meisje-RKG … meisje-PGD
- Een opdracht die voor NCZ 1 uur zedenleer plant: In feite plaatst die opdracht dan 2 subklassen op hetzelfde roosterpunt: meisje-NCZ, jongen-NCZ
Dus, elke opdracht die K plant, volledig of volgens bepaalde partitie-elementen plaatst alle of een deel van de 8 subklassen op een roosterpunt.
Waardespreidingen en Partities
De algemene regel is als volgt: Indien de selectiecriteria, die gebruikt worden om de opdrachten te selecteren, een klas (of klassen) bevat dan moeten de spreidingen per subklas bekeken worden en niet langer op het niveau van de klas.
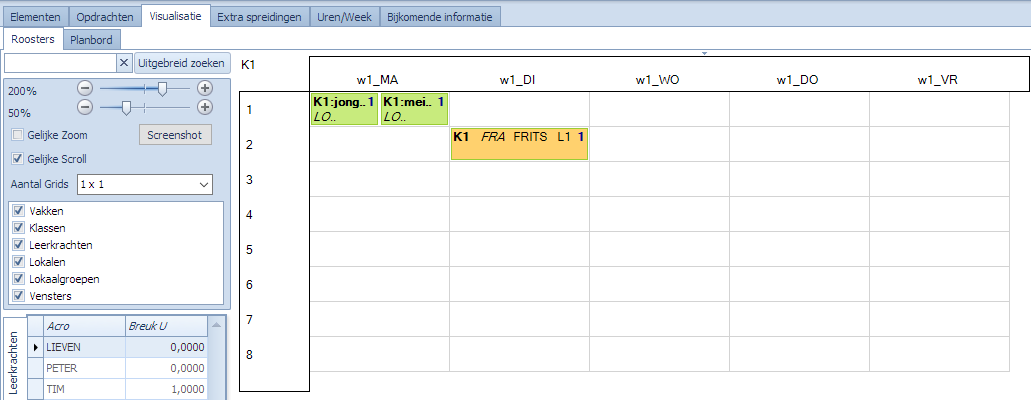
Stel dat men zegt dat de spreiding van LO voor K maximum 1 uur per dag mag zijn. Stel dat de meisjes LO hebben op maandag en de jongens ook. De meisjes bijvoorbeeld op ma1 en de jongens op ma2. Dit kan perfect met de partitie Geslacht geregeld worden. Beide lessen zijn dus aparte opdrachten. De vraag is nu “heeft K maar 1 uur LO per dag?”. In feite zie je K 2 keer op het roosters staan, een keer LO voor K:meisje, een keer LO voor K:jongen. Dus, de klas K staat er 2 keer op maar de leerlingen hebben inderdaad maar 1 keer LO op maandag.
Doordat de opsplitsing nu per klasgroep gebeurt zullen de spreidingen op de achtergrond uitgesplistst worden zodat K:meisje inderdaad maar 1 keer LO heeft en K:jongen ook maar 1 keer LO per dag heeft.
Nemen we als voorbeeld volgende opdrachten en spreiding:
Voor de gemakkelijkheid alle lessen in hetzelfde lokaal zodat we op L1 kunnen selecteren in de spreiding.
In de spreiding selecteren we nu alle opdrachten op basis van L1 en stellen dat er max 2 uur op maandag mag staan. We spreken in de spreiding dus niet van de klas K1.
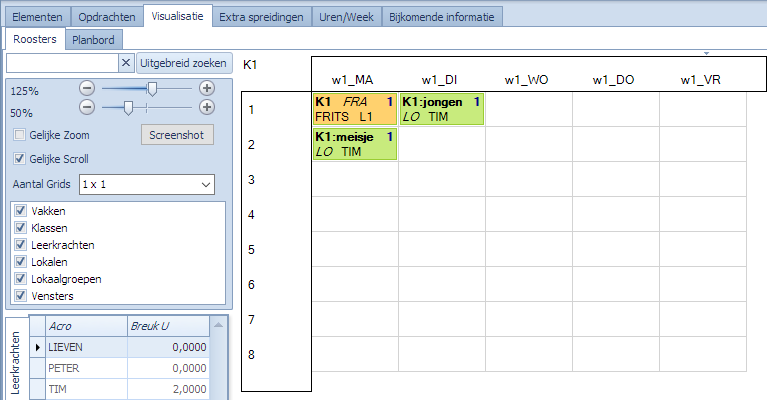
Bekijken we het resultaat nadat Mondriaan naar een oplossing gezocht heeft, zien we dat er op maandag inderdaad maar 2 keer een roosterpunt bezet is. Het derde is uitgeweken naar dinsdag.
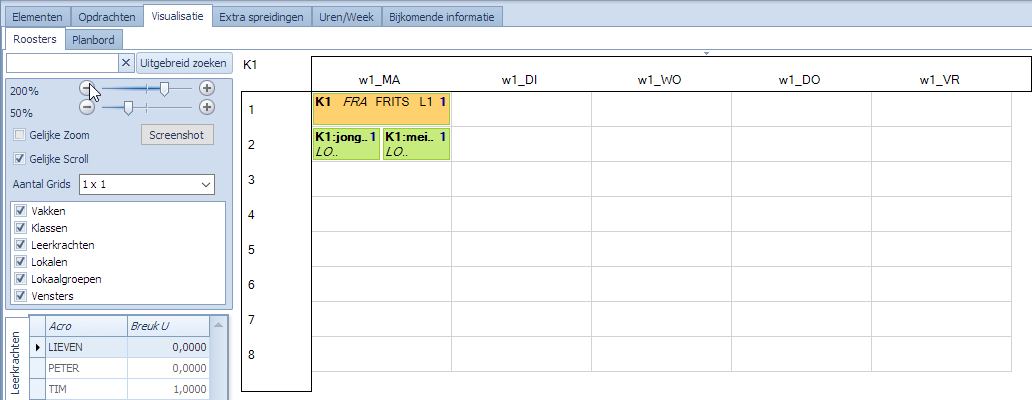
Herformuleren we de spreiding door K1 te gebruiken ipv L1 om dezelfde opdrachten te selecteren:
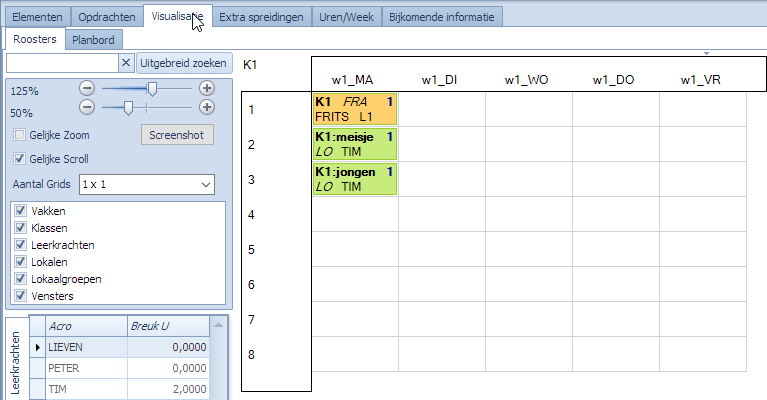
Bekijken we het resultaat nadat Mondriaan naar een oplossing gezocht heeft, zien we dat er op maandag 3 roosterpunten bezet zijn. Klopt dit? Ja, als we op het niveau van de subklassen kijken is dit inderdaad correct:
- Subklas K1-meisje staat op ma1, ma2
- Subklas K1-jongen staat op ma1, ma3
Dus, er is aan de eis voldaan.
Voorbeeld waarbij de partitie-elementen op hetzelfde moment kunnen vallen:
Indien we de opdrachten aanpassen zodat K1:jongen en K1:meisje elk in een ander lokaal zitten en een andere leerkracht hebben. Nu kunnen ze op hetzelfde roosterpunt staan.
We passen de spreiding aan zodat we nog steeds alle opdrachten selecteren zonder K1 te vermelden:
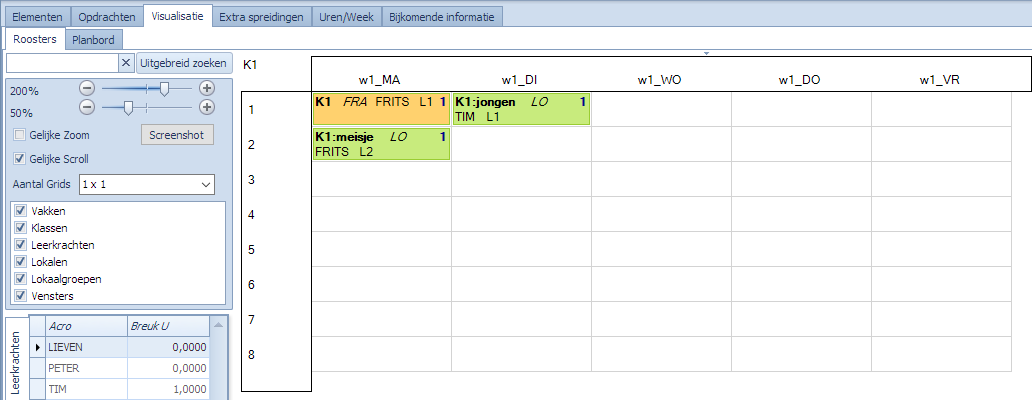
We tonen hier 2 mogelijke (van de vele) oplossingen waarbij we inderdaad zien dat de opdrachten nog steeds over 2 dagen verspreid zijn zodat maandag steeds maximaal 2 roosterpunten bezet zijn.
Wijzigen we de spreiding door expliciet K1 te vermelden dan wordt het gedrag weer anders en zal er per subklas gespreid worden:
Mogelijk resultaat: hier zien we dat elke subklas inderdaad maximaal 2 uur voorkomt op maandag.
Meer complexe voorbeelden waarbij eenzelfde klas volgens 2 of meerdere partities opgedeeld wordt laten we als oefening aan de gebruiker.
Extra Informatie:
Informatie over het feit dat waardespreidingen extra opgesplitst worden doordat opdrachten met verschillende partitie-elementen werken vindt men hier:
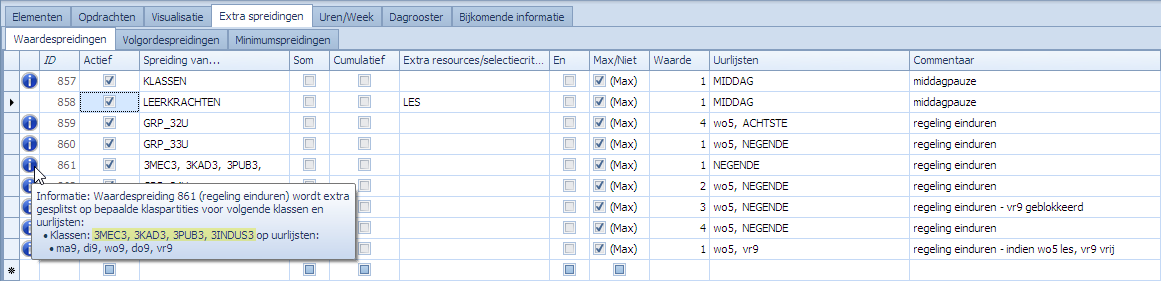
De blauwe “i” toon info over de spreiding. Kijken we naar de klas 3MEC3 in spreiding 861. We vragen via een spreiding max 1 maal les op het 9de uur. De opdrachten voor deze klas (en die voor deze spreiding in aanmerking komen) werken blijkbaar niet steeds met de volledige klas maar soms met partitie-elementen. Dwz dat de spreiding opgesplitst zal zijn per gecombineerd partitie-element om vanuit het standpunt van de leerling aan de spreiding te kunnen voldoen. Dat wordt getoond via deze informatie.
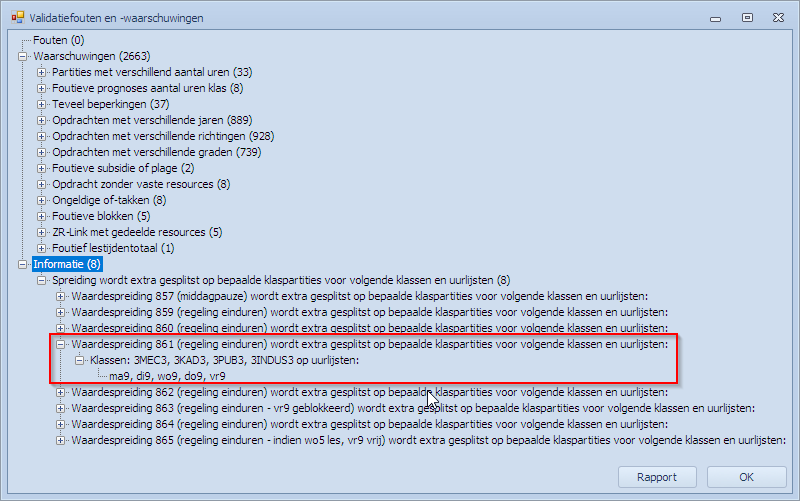
Ook bij “Valideer Invoer” zal men deze extra informatie kunnen vinden:
Verplaatsingen vermijden tussen locaties als voorbeeld van Partities met Waardespreidingen
Een van de vele toepassingen van waardespreidingen zijn verplaatsingen regelen. Hieronder verstaan we dat het bijvoorbeeld ongewenst is om een klas zich tussen verafgelegen locaties te laten verplaatsen op bepaalde momenten. Er zijn momenten dat het toegelaten is, maar op momenten waar er te weinig tijd is wordt dat best vermeden. Locaties worden gedefinieerd in de “Elementen | Lokalen” tab en elk lokaal kan men hier ook aan een locatie koppelen. Stel dat we een school hebben met 3 locaties. De locaties noemen we: PTSB, PTS3, PTSplus (voorbeeld van een bekende school). Stel dat we volgende verplaatsingen willen beperken:
- Tussen PTSB en PTS3
- Tussen PTSB en PTSplus
Voor leerkrachten en klassen willen we verplaatsingen op andere momenten beperken. Voor klassen laten we enkel toe dat ze over de middag verplaatsen, voor leerkrachten mag dat ook tussen het 2de en 3de uur en tussen het 6de en 7de uur. Als we zeggen dat een klas zich niet mag verplaatsen in de voormiddag dan kunnen we dat als volgt controleren: Neem 2 willekeurige uren uit de voormiddag (bv ma1 en ma3) en bekijk of hun locaties daar verschillend zijn. Indien zo dan hebben ze zich verplaatst en dat mag niet. Stel dat we deze controle a.d.h.v. een spreiding willen formuleren. We nemen dan alle opdrachten van die klas en koppelen aan de locaties waartussen we niet mogen verplaatsen de gewichten 1 en 2. Als uurlijst om op te tellen geven we (ma1,ma3). Indien de som op die 2 roosterpunten = 3 hebben we een niet toegelaten situatie. Is de som 2 of 4 dan zit die klas op beide roosterpunten op dezelfde locatie.
Voor klassen hebben we in dit voorbeeld VERPLAATSING_HD als uurlijst die alle te controleren uur-koppels bevat. Voor leerkrachten is dat KWART. In volgend scherm wordt via 4 eenvoudige waardespreidingen de verplaatsing geregeld.
Bekijken we de eerste lijn: we selecteren alle opdrachten waarin de locaties PSTB en PTSplus in voorkomen en geven het gewicht 1 en 2 aan de respectievelijke opdrachten. Als extra resource staat er KLASSEN en het vlagje “En” is uitgevinkt. D.w.z. dat we per klas de opdachten gaan bundelen. Per klas en per uur-koppel wordt de telling ter controle van de verplaatsing gedaan.
Stel dat een klas K1 géén partities bevat. In dat geval zijn er geen subklassen en moet de spreiding ook niet verder uitgesplitst worden.
Stel dat een klas K1 wel partities bevat, bijvoorbeeld volgens Geslacht. In dit geval kan er voor de subklas “K1-meisje” een 2-uurs opdracht zijn voor bijvoorbeeld LO en voor “K1-jongen” een andere opdracht voor LO. Deze 2 opdrachten zorgen er samen voor dat K1 LO krijgt. De opdrachten kunnen op hetzelfde of op verschillende roosterpunten liggen. Stel nu dat we geen opsplitsing zouden doen van de spreidingen volgens subklassen. Wat kan er dan bijvoorbeeld in het rooster staan en hoe reageert de spreiding hier dan op:
- ma1: K1-meisje (PTSB), K1-jongen (PTSB) ==> telt voor 2
- ma3: K1-meisje (PTSplus), K1-jongen (PTSplus) ==> telt voor 4
Samen geeft dat 6 en is volgens de spreiding dus in orde. Echter, beide subklassen hebben zich nu verplaatst en dat is niet de bedoeling.
Ander voorbeeld
- ma1: K1-meisje (PTSB) ==> telt voor 1
- ma3: K1-jongen (PTSplus) ==> telt voor 2
Samen geeft dat 3 en is volgens de spreiding dus NIET in orde. Echter, het gaat om aparte subklassen en dus heeft er in feite niemand een verplaatsing gemaakt. Ook dat was dus niet de bedoeling.
Indien we de spreidingen nu per subklas zouden splitsen dan klopt het plaatje wel. Dat is dan ook wat er gebeurt indien men KLASSEN als selectiecriteria gebruikt. We hernemen het voorbeeld:
- ma1: K1-meisje (PTSB), K1-jongen (PTSB) ==> subklas K1-meisje: telt voor 1, subklas K1-jongen: telt voor 1
- ma3: K1-meisje (PTSplus), K1-jongen (PTSplus) ==> subklas K1-meisje: telt voor 2, subklas K1-jongen: telt voor 2
Samen geeft dat voor K1-meisje: 3 en voor K1-jongen: 3. In beide gevallen NIET toegelaten.
Ander voorbeeld:
- ma1: K1-meisje (PTSB) ==> subklas K1-meisje: telt voor 1, subklas K1-jongen: telt voor 0
- ma3: K1-jongen (PTSplus) ==> subklas K1-meisje: telt voor 0, subklas K1-jongen: telt voor 2
Samen geeft dat voor K1-meisje: 1 en voor K1-jongen: 2. In beide gevallen WEL toegelaten.
Hier zagen we dus het belang van de opsplitsing van de waardespreidingen volgens de subklassen. De opsplitsing werd “geforceerd” door KLASSEN als selectiecriteria te gebruiken. Stel dat we KLASSEN niet gebruikt hadden maar wel een ander element (bv. voor elke klas maken we een varia aan en zetten die steeds mee in de opdracht) met hetzelfde effect op de selectie, dan zou de opsplitsing niet gebeuren per subklas en klopten de spreidingsregels helemaal niet meer.
Nog enkele tips
Opgepast met “Niet gelijk aan waarde” spreidingen
De MBE (Mondriaan Backtrack Engine) evalueert elke waardespreiding voor elke wijziging die hij in het rooster wenst aan te brengen. Van zodra een van de waardespreidingen een conflict meldt moet de engine een ander pad bewandelen om tot een oplossing te komen. Dit wil zeggen dat het eindresultaat, gevonden door de engine, aan alle waardespreidingen moet voldoen, maar, dat er ook een pad naar de oplossing moet bestaan waarbij het resultaat na elk genomen stapje ook moet voldoen aan al de waardespreidingen. Soms kan men waardespreidingen formuleren die inderdaad op het eindresultaat moeten gelden maar waarvoor er geen oplossingspad bestaat waarbij bij elke tussenstap aan die waardespreidingen voldaan wordt. Een voorbeeld om dit te illustreren:
Stel dat Peter les geeft in een school en dat hij in verschillende klassen komt voor een waaier aan vakken en dat zijn opdrachten allemaal in losse uren gegeven worden. Hij heeft geen blokuren. Stel dat men de vreemde eis stelt dat Peter op het 4de en 5de uur van de dag ofwel niet, ofwel 2 uur les geeft. Dus, men wenst te vermijden dat hij het 4de maar niet het 5de en ook niet het 5de maar niet het 4de uur les geeft. Een schijnbaar eenvoudige manier om die eis te formuleren is via een “Niet gelijk aan waarde” spreiding op volgende manier:
Hierbij nemen we alle opdrachten waar een klas bij betrokken is en waarbij we ook eisen dat Peter erbij betrokken is. Alle opdrachten worden samengeteld in de waardespreiding. De enige opsplitsende factor is de uurlijst. Die bestaat uit een OF-uurlijst van 5 paren van telkens het 4de en 5de uur. Bekijken we één uurlijst van 2 uur en alle opdrachten die we geselecteerd hebben. We eisen dat de som op die 2 uur verschillend is van 1. Dus, 0 is goed of 2 is goed. Dit zijn de enige 2 goede situaties.
- 0 kunnen we makkelijk bereiken door er nooit iets te zetten.
- 2 kunnen we enkel bereiken indien we er eerst 1 zetten en dan nog 1 omdat Peter met losse uren werkt. Echter, het eerste uur er plaatsen gaat nooit lukken want de waardespreiding zal op dat moment zeggen dat er een probleem is.
Dus, we zien duidelijk een gevaarlijke situatie waarbij we heel wat mogelijkheden laten verloren gaan. De situatie waarbij de 2 uren bezet zijn kunnen we nooit bereiken met losse uren. Dit is dus een eis die we zeker niet op deze manier moeten formuleren.
Opgelet: De MBE kan uitzonderlijk een “NIET gelijk aan waarde” spreiding niet respecteren
Indien men de MBE (versie BT10.00.12) een rooster laat bepalen en in de set van beperkingen zitten ook dit type van spreidingen dan kan het uitzonderlijk voorkomen dat aan dergelijke beperkingen niet voldaan wordt. Dit wordt dan ook gerapporteerd na het beëindigen van de MBE. Het is niet zo dat dit kan voorkomen bij elk type “NIET gelijk aan waarde” spreiding. Het kan enkel gebeuren indien de spreidingsregel geschonden kan worden door het wegnemen van een opdracht uit het rooster. Dit zijn echter zeer specifieke gevallen. Voor het klassieke gebruik, bijvoorbeeld voor het regelen van verplaatsingen, komt dat niet voor. Indien een dergelijke spreiding door en MBE niet gerespecteerd werd kan dat in een volgende run van de MBE weer opgelost worden.
Nog enkele weetjes over waardespreidingen
- Weet dat spreidingen geen wensen zijn maar bevelen. Het gaat niet om iets zo goed mogelijk te spreiden, het gaat om iets exact juist te spreiden en dit zonder toegevingen.
- Onthoud dat spreidingen niet alleen op het eindresultaat gecontroleerd worden maar ook tijdens het zoeken naar een oplossing. Om tot een oplossing te komen moet elke stap in de opbouw voldoen aan de spreidingsregels.
- Gebruik spreidingen niet overdadig.
- Weet dat de vakspreidingen in het Opdrachten tabblad ook waardespreidingen zijn die men echter niet in het tabblad “Extra spreidingen” te zien krijgt.
- Weet dat de vakspreidingen in het Opdrachten tabblad lokaal gelden, enkel van toepassing zijn op de opdracht waar ze bijstaan in het opdrachten tabblad.
- Weet dat er consequenties verbonden zijn aan het gebruiken van klassen als selectiecriteria voor opdrachten in spreidingen indien deze klassen opgedeeld zijn in partities. Denk aan de verplaatsingsproblematiek waar het noodzakelijk is om de klassen zelf mee in de selectiecriteria op te nemen.
Toepassingsgebieden voor waardespreidingen
Een kleine greep uit de mogelijke toepassingsgebieden:
- Spreiden van vakken in de week per klas. Dit wordt meestal via vakspreidingen in het Opdrachten tabblad geregeld.
- Spreiden van aantal uren dat een leerkracht per dag les geeft (minder frequent gebuikt).
- Garanderen dat een leerkracht middagpauze heeft voor scholen die les geven over de middag.
- Regelen van verplaatsingen tussen verschillende vestigingen van een school en dit voor zowel de leerkrachten als de klassen.
- Regelen van inhaallessen in roosters met roulatiesystemen (wordt regelmatig gebruikt in verpleegsterscholen).
- Regelen van complexere LO roulatiesystemen waar er kleine beschikbaarheid is van turnzalen en zwembaden.
- etc…