Opdrachten beperken door volgordespreidingen
Inhoud
- Inleiding
- De essentie van de volgordespreiding
- Mechanisme achter de volgordespreidingen in detail
- Groepen gebruiken in de “Selectie 1” en “Selectie 2” kolommen
- Mogelijkheden om in één lijn verschillende volgordespreidingen te definiëren
- Nog enkele voorbeelden
- Nog enkele tips
Inleiding
Opdrachten worden normaal in hun mogelijkheden beperkt door volgende statische beperkingen:
- Mogelijke startpunten van de blokken/uren die geplaatst moeten worden.
- Inherente beperkingen die aan de individuele resources van de opdracht opgelegd worden. Een leerkracht kan bijvoorbeeld niet op dinsdag aanwezig zijn.
Naast statische beperkingen zijn er dynamische beperkingen die de opdracht ondervindt tijdens het roosteren:
- Onbeschikbaarheid van resources op bepaalde momenten omdat andere opdrachten die resources al geplaatst hebben op die momenten.
- Eventueel beperkingen opgelegd door een venster waar de opdracht in geplaatst moet worden. Andere factoren kunnen de locatie van dat venster beperken.
- Eventueel beperkingen opgelegd door een “zelfde roosterpunt link” (ZR-Link) waarbij de plaats mee bepaald kan worden door andere opdrachten die in diezelfde roosterpunt link participeren.
Zowel deze statische als dynamische beperkingen zijn gebaseerd op de beschikbaarheid van resources op roosterpunten. Door in opdrachten resources samen te zetten moet automatisch aan een heel deel voorwaarden voldaan worden, opdat zulk een opdracht op een bepaald roosterpunt geplaatst kan worden.
Roosters die gemaakt worden op basis van dergelijke opdrachten garanderen dat er geen dubbele bezetting is van resources en garanderen eventueel nog enkele andere beperkingen zoals het samen in een venster zitten van opdrachten of op hetzelfde moment vallen in het rooster via een ZR-link.
Deze resourcebeperkingen (en startuurlijstbeperkingen) zijn vaak niet voldoende om de roosters te bekomen die men wenst. Het belangrijkste type bijkomende beperking is de “waardespreiding”. Deze wordt uitvoerig toegelicht op de pagina “Opdrachten beperken door waardespreidingen“.
Een ander type beperking zijn de “volgordespreidingen”. Dit is een eenvoudiger type beperking dan de “waardespreiding” en wordt minder vaak toegepast maar kan in sommige gevallen erg nuttig zijn.
Met een volgordespreiding kan men de volgorde tussen opdrachten afdwingen binnen een bepaald tijdsinterval of periode.
Eenvoudig voorbeeld: een klas 6A heeft een praktijkvak EL_P met daaraan gelinkt een theorievak EL_T. Deze vakken mogen eender waar in de week vallen maar de theorie moet voor de praktijk komen. Er wordt dus niet gevraagd dat ze aansluitend tegen elkaar liggen, dat is niet nodig. Het enige wat van belang is, is de volgorde binnen de roosterweek.
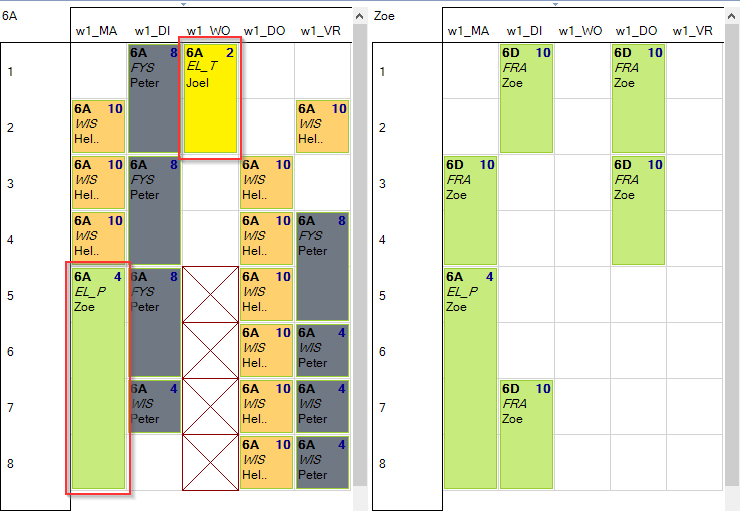
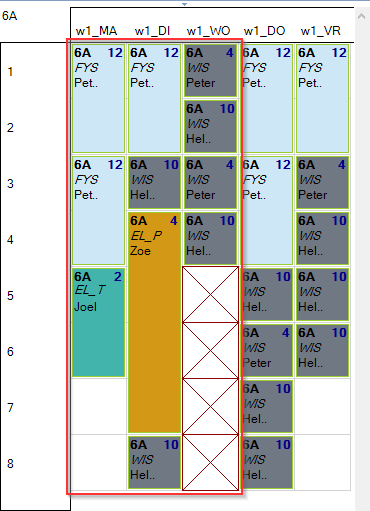
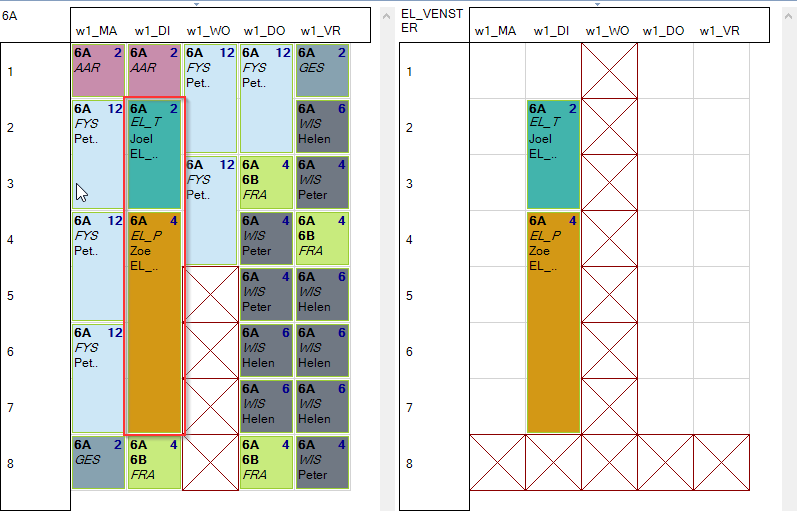
In volgend plaatje ziet men links het rooster van 6A met daarin een aantal opdrachten waaronder ook EL_T (blok van 2 uur) en EL_P (blok van 4 uur). Er werden geen extra beperkingen aan de opdrachten opgelegd waardoor ze willekeurig in dit rooster terechtkomen. In dit geval duidelijk niet zoals gewenst. EL_P ligt vóór EL_T in het rooster. Dit willen we uitsluiten.
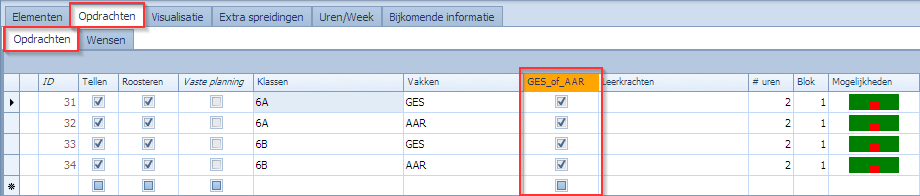
In het tabblad “Extra spreidingen | Volgordespreidingen” kan men volgordebeperkingen definiëren.
In deze volgordespreiding hebben we 2 selecties van opdrachten waartussen we een beperking definiëren:
- Selectie 1: de opdracht(en) van 6A waar het vak EL_T in voorkomt.
- Selectie 2: de opdracht(en) van 6A waar het vak EL_P in voorkomt.
Merk op dat de selectie van de opdrachten eenvoudig gehouden is. Met het vlagje “En Selectie 1” kan men aanduiden of de gebruikte selectiecriteria in “Selectie 1” allemaal aanwezig moeten zijn in een geselecteerde opdrachten of dat minstens één van de selectiecriteria aanwezig moet zijn in een geselecteerde opdracht. In het voorbeeld (6A, EL_T) willen we dus enkel de opdrachten waar zowel 6A ald EL_T in voorkomt. Dezelfde redenering geldt voor het vlagje “En Selectie 2”.
In de kolom “Type” geven we aan welk soort volgorde we tussen de opdrachten van “Selectie 1” en “Selectie 2” willen afdwingen. Mogelijke waarden zijn “Voor”, “Na”, “Geen overlap”. In het voorbeeld gebruiken we “Voor”. Hiermee duiden we aan dat de opdracht(en) uit “Selectie 1” vóór de opdrachten uit “Selectie 2” moeten liggen in het interval of periode die we in de kolom “Uurlijsten” vinden. In het voorbeeld gebruiken we als interval de uurlijst “WEEK”. Dit is een eenvoudige uurlijst die alle uren van de week bevat. Een andere optie voor de uurlijst kan ook “WEEK_PERIODE” zijn. Hier hebben we enkel het eerste en laatste uur van de periode gedefinieerd. Dat is voldoende. Volgordespreidingen controleren de volgorde binnen één of meerdere periodes en een periode wordt gedefinieerd door een begin en een eindpunt. Van de opgegeven uurlijst is dus enkel het eerste en laatste uur van belang voor het definiëren van een periode. Vandaar dat “WEEK” en “WEEK_PERIODE” beide gebruikt kunnen worden en hetzelfde effect zullen hebben.
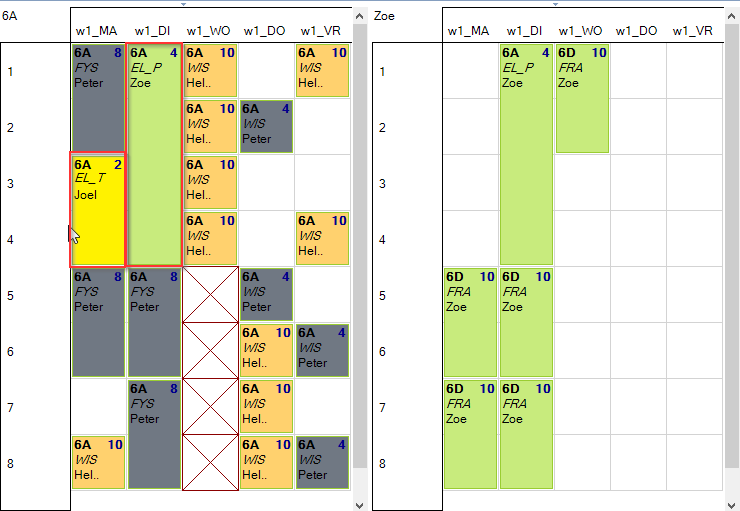
Laten we de Mondriaan engine een oplossing berekenen voor dit probleem dan is dit een mogelijke oplossing:
Het vak EL_T staat nu op maandag en EL_P op dinsdag. Er is dus aan de eis voldaan.
De essentie van de volgordespreiding
Een volgordespreiding is een zeer eenvoudig concept. In de basis is het als volgt uit te leggen:
- van 2 welbepaalde disjuncte sets van opdrachten, door de gebruiker te bepalen
- bepaalt men voor beide sets en op elk moment het eerste en laatste bezette uur in het rooster
- waarbij enkel gekeken wordt naar uren die binnen een door de gebruiker te bepalen interval of periode vallen
Vervolgens legt men een eis op aan de relatie tussen die eerste en laatste bezette uren voor beide sets. Er zijn 3 soorten eisen die men kan opleggen:
- “Voor”: ofwel moet het laatst bezette uur van set 1 vóór het eerste bezette uur van set 2 liggen
- “Na”: ofwel moet het eerst bezette uur van set 1 na het laatste bezette uur van set 2 liggen
- “Geen overlap”: ofwel “Voor” of “Na” waarbij de keuze een Mondriaan gelaten wordt
Betekenis het “eerste bezette uur” binnen een set van opdrachten binnen een interval: men neemt alle opdrachten van set 1 en kijkt waar deze opdrachten staan in het rooster binnen het gedefinieerde interval. Dan zoekt men binnen dit interval en over al deze opdrachten heen het eerste uur dat bezet is. Voor het “laatste bezette uur” geldt dezelfde redenering: men neemt alle opdrachten van set 1 en kijkt waar deze opdrachten staan in het rooster binnen het gedefinieerde interval. Dan zoekt men binnen dit interval en over al deze opdrachten heen het laatste uur dat bezet is.
Merk op dat de “Geen overlap” eis pas echt zin heeft indien er in set 1 of set 2 minstens 2 opdrachten zitten. Indien er in set 1 en set 2 maar één opdracht zit dan heeft “Geen overlap” als enige effect dat beide opdrachten niet op hetzelfde moment kunnen vallen. Dit zou op zich ook een nuttige toepassing kunnen hebben maar dergelijke eis legt men normaal makkelijker op via een waardespreiding of via een variatype.
Tijdens het roosteren (er wordt een oplossing gezocht door de engine van Mondriaan) worden alle volgordepreidingen permanent geëvalueerd. Van zodra het plaatsen van een opdracht een volgordespreiding zou schenden moet de engine een andere oplossing kiezen.
De complexiteit van volgordespreidingen in het tabblad “Extra Spreidingen | Volgordespreidingen” zit voornamelijk in volgende aspecten:
- Om het voor de gebruiker handiger te maken kan men patronen van volgordespreidingen opgeven in één enkele regel in Mondriaan.
- De eerste patronen die men kan maken zijn op basis van de uurlijsten. Hier kan men meerdere intervallen opgeven in één OF-uurlijst. Geeft men een OF-uurlijst dan definieert men meerdere intervallen of periodes waarbinnen de volgorde gecontroleerd wordt.
- Een tweede vorm van patronen kan men maken indien men in “Selectie 1” en/of “Selectie 2” groepen gebruikt. Gebruikt men daar een groep dan ken men die ook vermelden in de kolom “Opsplitsing” om aan Mondriaan te laten weten dat die groep geïnterpreteerd moet worden als een opsplitser voor de spreidingsregel. Vermeldt men die groep niet in “Opsplitsing” dan blijft de groep zijn normale rol vervullen in de spreiding.
- De andere kolommen “En Selectie 1”, “En Selectie 2” geven nooit aanleiding tot een ontdubbeling van opdrachten in aparte volgordespreidingen.
- Voor “Selectie 1” en “Selectie 2” kan men via de vlagjes “En Selectie 1” en “En Selectie 2” beslissen of aan alle dan wel minstens één van de selectie criteria moet voldaan zijn opdat een opdracht geselecteerd zou worden.
Mechanisme achter de volgordespreidingen in detail
volgordespreidingen worden door de gebruiker gedefinieerd in het tablad “Extra spreidingen | Volgordespreidingen”. Bekijkt men één enkele volgordespreiding dan bestaat die steeds uit volgende elementen:
- Twee disjuncte sets (1 en 2) van opdrachten die participeren in de volgordespreiding.
- Een interval waarbinnen de volgordespreiding gecontroleerd wordt.
- Een type volgordespreiding (Voor, Na, Geen overlap).
Volgende beschrijving geeft in meer detail weer wat er gecontroleerd wordt voor een volgordespreiding:
Merk op dat volgende constructies exact gelijk zijn:
- Set 1 “Voor” Set 2
- Set 2 “Na” Set 1
Dus, als men de sets van plaats verwisselt en men wisselt het type ook van “Voor” naar “Na” of omgekeerd dan geeft dat hetzelfde resultaat.
Groepen gebruiken in de “Selectie 1” en “Selectie 2” kolommen
We kunnen ook groepen gebruiken in deze kolommen. In het “Elementen | [Groepen]” tabblad kan men groepen aanmaken en een van de aspecten van groepen is dat een “EN” of een “OF” groep kunnen zijn. Dit aspect heeft voor de kolommen “Selectie 1” en “Selectie 2” geen betekenis. Het enige wat een rol speelt zijn de echte elementen die in die groepen (of groepen van groepen) zitten. Enkel de vlagjes “En Selectie 1” en “En Selectie 2” bepalen of de selectie van de opdrachten moeten gebeuren op basis van een “EN” of “OF” logica.
Mogelijkheden om in één lijn verschillende volgordespreidingen te definiëren
Zoals eerder aangehaald kunnen we bij volgordespreiding via
- de Uurlijsten kolom meerdere volgordespreidingen in één lijn schrijven.
- de Opsplitsing kolom een groep laten interpreteren als opsplitser en dus ook meerdere volgordespreidingen in één lijn schrijven.
Volgordespreidingen combineren op basis van de kolom “Uurlijsten”
Als je 2 of meerdere lijnen in het tabblad “Volgordespreidingen” hebt die enkel verschillen in de Uurlijst die ze bevatten dan kan men ze groeperen door de uurlijsten te combineren in een OF-constructie. Merk op dat de uurlijst het interval voorstelt waarbinnen de volgordespreiding gecontroleerd wordt.
Voorbeeld: We hebben 5 lijnen met volgordespreidingen waarbij het enige verschil de uurlijst is. Elk van deze volgordespreidingen stelt dat FYS in 6A steeds vóór WIS in 6A moet vallen. De eerste lijn stelt dat dat waar moet zijn voor maandag. De tweede voor dinsdag, etc.
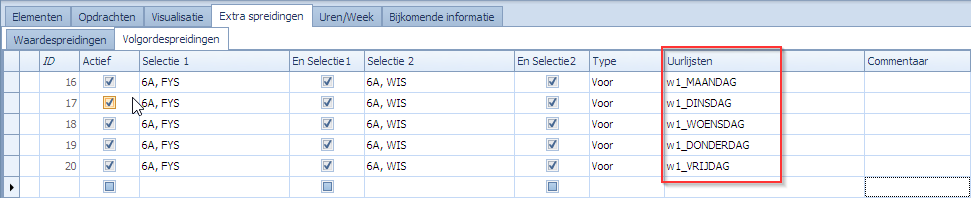
Een verkorte schrijfwijze voor deze 5 volgordespreidingen is de volgende:
Belangrijk is dat de nieuwe uurlijst juist gedefinieerd wordt als een OF-constructie van die 5 oorspronkelijke dagen:
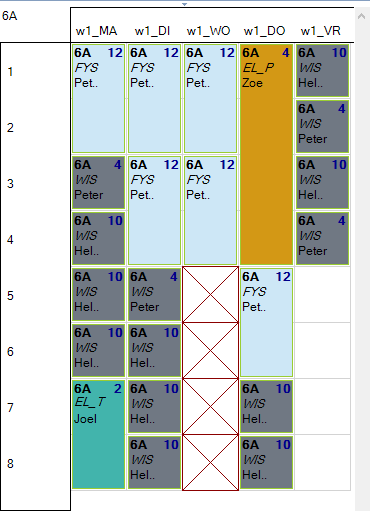
Een mogelijke oplossing voor dit probleem wordt getoond in volgend plaatje:
Voor elk van de weekdagen geldt inderdaad dat FYS steeds vóór WIS geplaatst is.
Volgordespreidingen combineren op basis van de kolom “Opsplitsing”
In de kolom “Opsplitsing” kan men groepen zetten die in de kolom “Selectie 1” en/of “Selectie 2” vermeld worden. Als men een groep in de kolom “Opsplitsing” zet dan wordt die groep aanzien als een middel om de spreiding op te splitsen volgens de elementen in die groep. Op deze manier kan men dus op een verkorte schrijfwijze meerdere volgordespreidingen definiëren.
Voorbeeld: in volgend praktijkvoorbeeld hebben we een school met 3 locaties met de namen SED, SEA, en SMD. Leerkrachten kunnen op elk van die locaties lesgeven. Omdat de locaties op een redelijke afstand van elkaar liggen is het niet handig dat leerkrachten vaak moeten wisselen van locatie. Via waardespreidingen kan men bepalen op welke momenten leerkrachten van locatie kunnen wisselen. Dit is typisch tijdens de pauzes (tussen uur 2-3, 4-5, 5-6, 7-8 in het voorbeeld). Deze beperking zorgt ervoor dat tenminste de leerlingen nooit op hun leerkracht moeten wachten. Hier ziet men het rooster van 2 leerkrachten STS en PAC waarbij de opdrachten ingekleurd zijn volgens de locaties (3 kleuren).
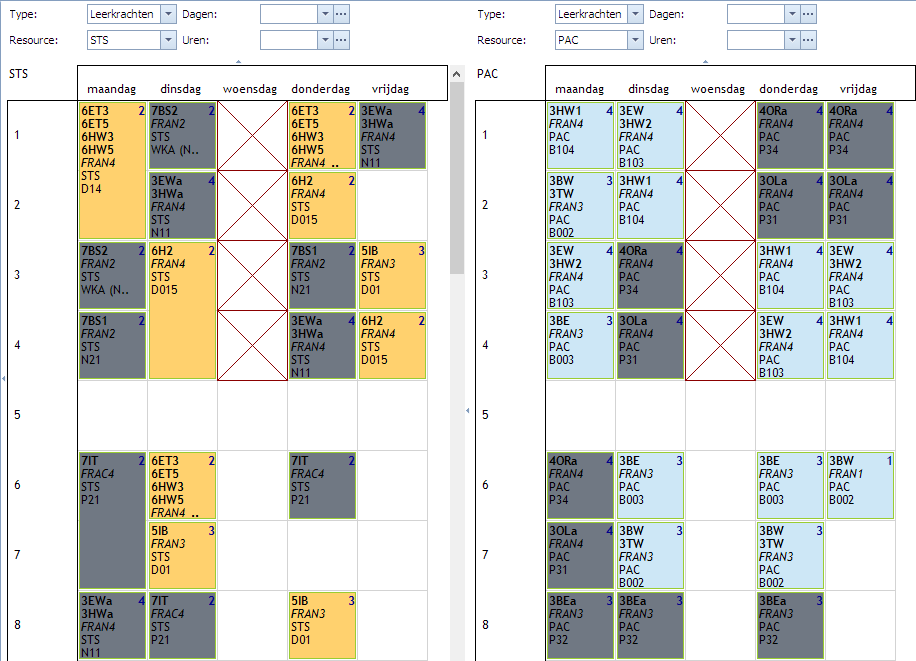
Er is inderdaad voldaan aan de regel dat leerkrachten zich enkel tijdens de pauzes verplaatsen. Echter, dit gebeurt te vaak. Op deze manier hebben leerkrachten zelf weinig aan hun pauzes. We willen dit beperken tot maximaal 1 verplaatsing per dag.
We zouden dit voor deze 2 leerkrachten als volgt kunnen bekomen via volgordespreidingen:

Voor leerkracht STS zeggen we dat er op geen enkele dag een overlap mag zijn tussen zijn:
- opdrachten op locatie SED en SEA
- opdrachten op locatie SED en SMD
- opdrachten op locatie SEA en SMD
Voor leerkracht PAC zeggen we daarna exact hetzelfde. Als we meerdere leerkrachten hebben gaan we dat dus telkens moeten herhalen, telkens 3 volgordespreidingen. Plannen we het rooster met deze extra volgordespreidingen zien we het volgende:
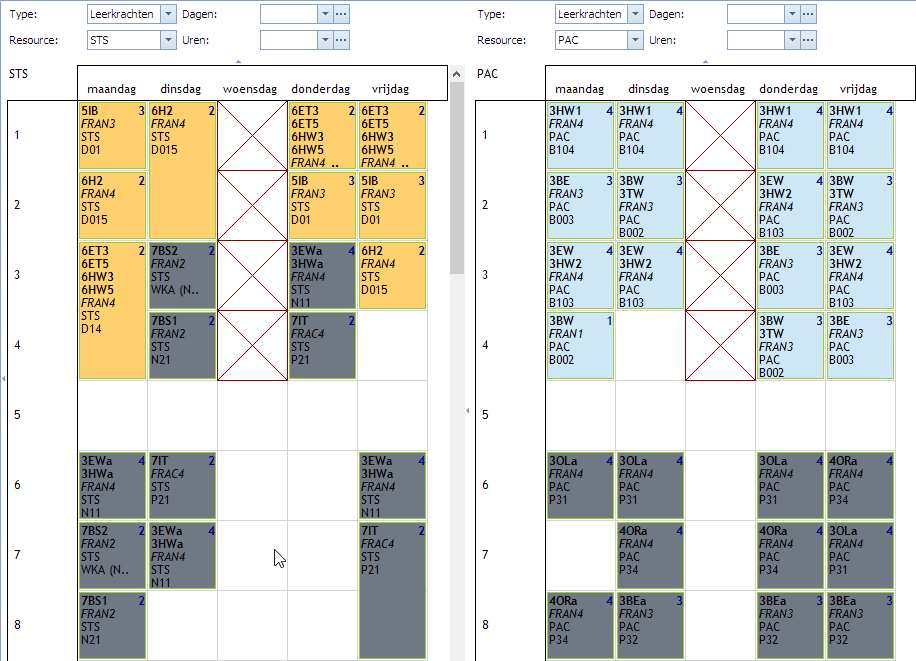
Dit geeft het gewenste resultaat, maximaal 1 verplaatsing per dag. Blijft wel het probleem dat het veel invoerwerk is. Dit kunnen we oplossen door een groep van leerkrachten te maken en die groep aan te duiden als Opsplitsing:

We geven de groep een naam en zetten er alle leerkrachten in waarvoor we die spreidingen willen aanmaken. We hebben die 6 volgordespreidingen nu vervangen door 3. De groep vermelden we nu op de plaatsen waar de leerkrachten eerst stonden en zetten hem ook in de kolom “Opsplitsing”. Nu weet Mondriaan dat het om een patroon gaat en dat elke spreidingsregel opgesplitst mag worden volgens die groep.

Wenst men nog extra leerkrachten toe te voegen aan deze spreiding dan zet men ze gewoon mee in de groep.
Merk op dat als men de groep niet zou vermelden in de kolom “Opsplitsing” dat de spreiding ook een heel andere betekenis zou krijgen. In dit geval zouden we alle opdrachten waarin STS en PAC samen lesgeven niet laten overlappen en dat heeft in dit geval geen betekenis omdat ze niet samen in opdrachten voorkomen.
Men kan ook meerdere groepen gebruiken. Elk van de gebruikte groepen kan men in Opsplitsing zetten indien men de bedoeling heeft om hem als een patroon te zien.
Nog enkele voorbeelden
Voorbeeld: we wensen dat alle FYS opdrachten vóór alle WIS opdrachten komen indien ze tussen het eerste uur van maandag en het laatste uur van woensdag vallen.
In het rode kader wordt inderdaad aan deze eis voldaan. Alle FYS komt vóór WIS.
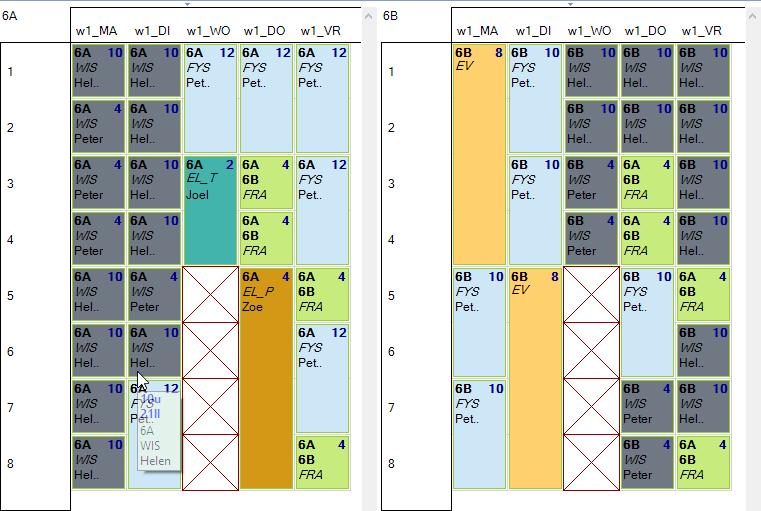
Voorbeeld: we wensen dat alle WIS opdrachten in 6A vóór alle WIS opdrachten in 6B komen binnen de ganse week en onafhankelijk van wie WIS geeft.
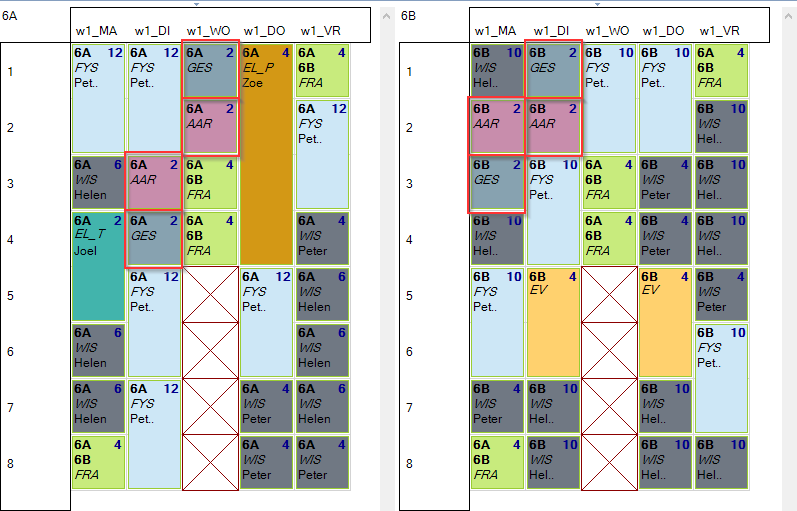
Een mogelijke oplossing voor 6A en 6B zou er dan als volgt kunnen uitzien.
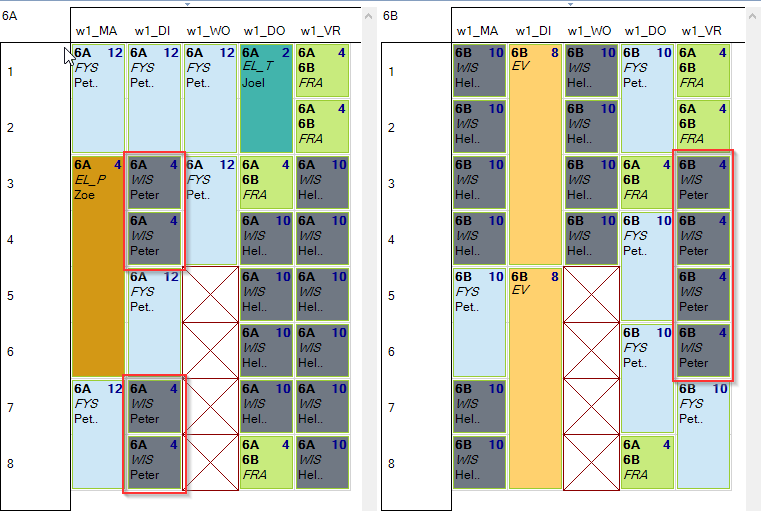
Voorbeeld: we wensen dat alle WIS opdrachten gegeven door Peter in 6A vóór alle WIS opdrachten gegeven door Peter in 6B komen binnen de ganse week.
Een mogelijke oplossing voor 6A en 6B zou er dan als volgt kunnen uitzien. De rode kaders tonen WIS gegeven door Peter.
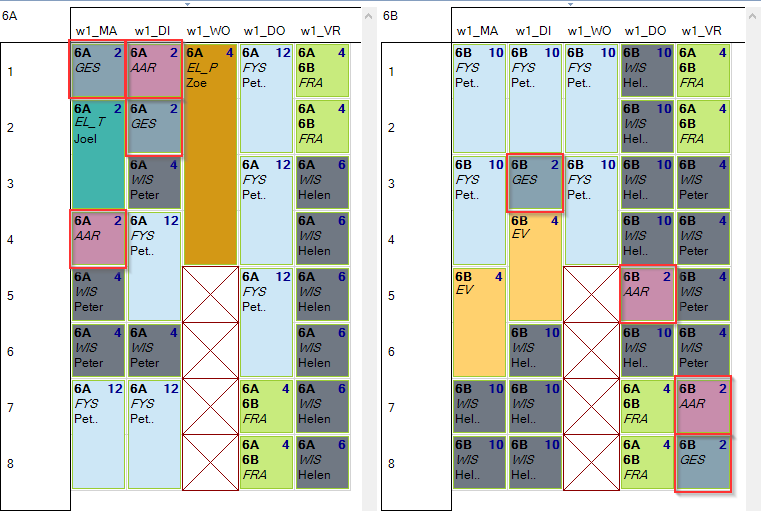
Voorbeeld: we wensen dat alle GES en AAR opdrachten in 6A vóór alle GES en AAR opdrachten in 6B komen binnen de ganse week.
Voor set 1 moeten we opdrachten selecteren waar 6A in voorkomt en waar AAR of GES in voorkomt.
- (6A, GES of AAR) moet vóór (6B, GES of AAR)
Dat is een constructie die we momenteel niet kunnen maken. Ook voor Set 2 geldt dit. Voor een “Voor” of “Na” volgordespreiding kunnen we dit eenvoudige oplossen door alle combinaties uit te schrijven:
- (6A, GES) moet vóór (6B, GES)
- (6A, AAR) moet vóór (6B, GES)
- (6A, GES) moet vóór (6B, AAR)
- (6A, AAR) moet vóór (6B, AAR)
Dat ziet er dan als volgt uit:
Een mogelijke oplossing ziet er dan als volgt uit:
Een andere manier om de opdrachten voor Set 1 en Set 2 te selecteren zou via een custom kolom in het opdrachten tabblad kunnen zijn.
Voorbeeld: we wensen dat alle GES en AAR opdrachten in 6A ofwel vóór ofwel na alle GES en AAR opdrachten in 6B komen binnen de ganse week.
Dit is een variatie op het vorige voorbeeld maar waarbij de toen gekozen oplossing om de opdrachtselectie te doen niet meer opgaat. We willen nl dat alle AAR/GES opdrachten van 6A ofwel voor ofwel na alle geselecteerde opdrachten van 6B liggen. Dat gaat niet op deze manier
Er is ook geen mogelijkheid om het in één lijn te schrijven omdat we zowel voor Selectie 1 als voor Selectie 2 een combinatie van een “of” en een “en” constructie nodig hebben.
- (6A, GES of AAR) moet vóór of na (6B, GES of AAR)
De enige manier om dit op te lossen is via een custom kolom in het opdrachten tabblad waar we de opdrachten GES en AAR een label geven waarmee we de selectie in één keer kunnen doen. Er zijn verschillende manieren op dit op te lossen. In dit voorbeeld maken we een custom kolom aan (GES_of_AAR) van het type “vlag” en markeren de opdrachten die GES or AAR opdrachten zijn.
Vervolgens gebruiken we de custom kolom CC_GES_of_AAR in de selectie van beide sets. Omdat we in het opdrachten tabblad geen onderscheid gemaakt hebben tussen 6A en 6B voor de custom kolom moeten we in de selectie nog steeds de klas vermelden en de “En Selectie x” vlagjes aanzetten.
Een mogelijke oplossing ziet er dan als volgt uit:
Mondriaan heeft de keuze gemaakt om alle geselecteerde opdrachten van 6A na alle geselecteerde opdrachten van 6B te plaatsen.
Opmerking: men zou foutief kunnen denken dat we dit ook zouden kunnen oplossen van een OF-groep van vakken te maken (GES en AAR in één OF-groep) en deze groep dan als selectieelement te gebruiken naar de klas. Dat gaat niet omdat het EN of OF karakter van een groep niet onderkend wordt in deze selecties zoals eerder aangehaald.
Voorbeeld: In 6A hebben we EL_T voor 2 uur en EL_P voor 4 uur. We eisen dat EL_T vóór EL_P komt en dat ze aansluitend liggen.
Merk op dat we in dit geval geen gebruik kunnen maken van een Bloklink zoals uitgelegd bij opdrachten omdat we hier niet dezelfde leerkracht gebruiken voor beide vakken. Een mogelijke oplossing is een combinatie van een volgordespreiding met een venster. Een venster van 6 uur houdt de opdrachten bij elkaar en de volgordespreiding verzekert dat EL_T eerst komt.
We definiëren een venster van 6 uur dat op de eerste 3 uur van de dag kan beginnen. We doen dit in het tabblad “Elementen | Vensters”
We passen de EL_T en EL_P opdrachten voor 6A aan door er het venster aan toe te voegen in het tabblad “Opdrachten | Opdrachten”.
De volgordespreiding definiëren we als voordien:
Een mogelijke oplossing ziet er dan als volgt uit:
Nog enkele tips
Nog enkele weetjes over volgordespreidingen
- Weet dat spreidingen geen wensen zijn maar bevelen. Het gaat niet om een volgorde zo goed mogelijk te benaderen, het gaat om een strikte volgorde en dit zonder toegevingen.
- Onthoud dat volgordespreidingen niet alleen op het eindresultaat gecontroleerd worden maar ook tijdens het zoeken naar een oplossing. Om tot een oplossing te komen moet elke stap in de opbouw voldoen aan de volgordespreidingsregels.
- Onthoud dat beide sets opdrachten geen gemeenschappelijke opdrachten mogen bevatten. Ze moeten maw disjunct zijn.
- Gebruik volgordespreidingen niet overdadig.
Toepassingsgebieden voor volgordespreidingen
Een kleine greep uit de mogelijke toepassingsgebieden:
- Vakken binnen een klas ten opzichte van elkaar in een bepaalde volgorde dwingen
- Leerkrachten over klassen heen in een bepaalde volgorde dwingen
- Verplaatsingen van leerkrachten/klassen tussen verschillende locaties beperken
- etc.