Opdrachten beperken door minimumspreidingen
Veel concepten die hier gebruikt of vermeld worden zijn reeds uitvoerig besproken op volgende pagina’s:
Details over het tabblad “Extra spreidingen | Minimumspreidingen” kan men vinden op de pagina “Definiëren van Minimumspreidingen“.
Inhoud
- Inleiding
- Enkele voorbeelden
- Resources waarvoor minimumspreidingen gedefinieerd kunnen worden
- De MBE ondersteunt géén minimimspreidingen voor keuzeresources
- Plan, Plan selectie en Analyse
- Opties in het optie-tabblad
- Het grote verschil met waardespreidingen (achter de schermen)
- Nog enkele tips over minimumspreidingen
Inleiding
Een minimumspreiding is een beperking die men oplegt aan een individuele resource over een bepaalde uurlijst in zijn rooster. Het eenvoudigste (en meest gebruikte) voorbeeld is een “minimum 2 uur per dag, of niets” beperking die men aan een leerkracht kan opleggen. Wat men in dit geval tracht te vermijden is dat iemand voor één uur les op een dag naar school zou moeten komen. Via een minimumspreiding kan men bijvoorbeeld volgende beperkingen opleggen voor de lesopdrachten van leerkracht ANKE:
- als ANKE maandag les geeft, dan moet dat voor minstens 2 uur zijn.
- als ANKE dinsdag les geeft, dan moet dat voor minstens 2 uur zijn.
- …
- als ANKE vrijdag les geeft, dan moet dat voor minstens 2 uur zijn.
Of korter geschreven:
- als ANKE op een dag les geeft, dan moet dat voor minstens 2 uur zijn.
Wat duidelijk moet zijn is dat géén les geven op een dag perfect in orde is maar dat één uur les niet is toegelaten; het moeten er dan minstens 2 zijn. In dit voorbeeld hebben we nu 2 gebruikt maar dat kan evengoed 3, 4, … zijn. We gebruiken in dit voorbeeld ook de dagen als uurlijsten waarop de beperking moet gelden maar dat kan eender welke uurlijst zijn.
Merk op dat men de beperking “Minimum 2 uur per dag, of niets” ook kan schrijven als “Niet 1 uur per dag“.
En zo kan men ook “Minimum 3 uur per dag, of niets” schrijven als:
- Niet 1 uur per dag, en
- Niet 2 uur per dag
Omdat een beperking van het type “Minimum x op een uurlijst U, of niets” achter de schermen vertaald wordt naar dergelijke “Niet y op uurlijst U” basisbeperkingen hebben we er in Mondriaan voor gekozen om ook meteen deze basisbeperkingen bijkomend als mogelijkheid aan te bieden.
Dus, in het tabblad “Extra spreidingen | Minimumspreidingen” kan men 2 soorten beperkingen aan individuele resources opleggen:
- Min x op uurlijst U, of niets.
- Niet x op uurlijst U
De eerste soort wordt door Mondriaan achter de schermen in termen van de 2de soort vertaald.
De aandachtige lezer die ook vertrouwd is met waardespreidingen zal zich afvragen waarom het concept “Niet” spreiding nu op 2 plaatsen kan voorkomen. Bij waardespreidingen kunnen we kiezen tussen “Max” of “Niet”, bij minimumspreidingen kan men kiezen tussen “Min” of “Niet”. Dat is dus op 2 plaatsen. Bij waardespreidingen legt men dergelijke beperkingen op aan een set van opdrachten, bij minimumspreidingen ook maar dan beperkt tot de lesopdrachten van één resource. Moest men dus bij waardespreidingen de opdrachten van één resource selecteren en daar een Min spreiding aan opleggen is het dan hetzelfde? Neen. We komen verder terug op het fundamentele verschil tussen de “Niet” spreiding bij de waarde- en bij de minimumspreiding.
Enkele voorbeelden
Voor we verder ingaan in de details enkele voorbeelden. We vertrekken van een bestaand rooster en bekijken de roosters van deze 3 leerkrachten. We zien dat elk van hen op een of meerdere dagen maar voor één uur naar school moeten komen. Dergelijke geïsoleerde uren kunnen vermeden worden via een minimumspreiding.
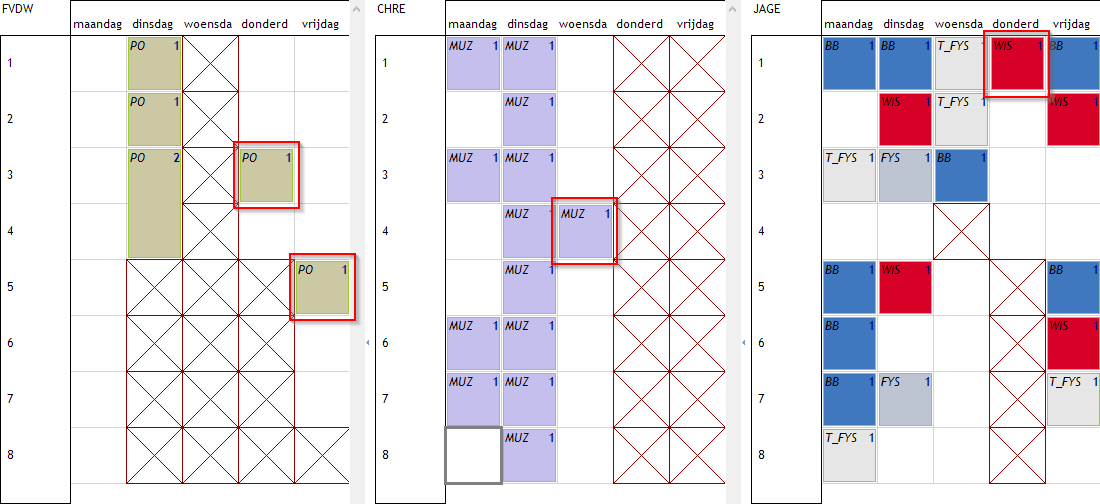
Voorbeeld 1: voor 3 leerkrachten – Minimum 2 uur les per dag, of niets
In het tabblad “Extra spreidingen | minimumspreiding” maken we een minimumspreiding aan voor deze 3 leerkrachten:

In “Resources” vermelden we de 3 leerkrachten. We kunnen dat ook via een groep van leerkrachten doen en we kunnen ook per leerkracht één lijn aanmaken in dit tabblad. Omdat het voor elke leerkracht hetzelfde moet zijn kunnen we alles samen zetten (verkorte schrijfwijze). We wensen Min 2 uit te drukken en dat op elke dag van de week. Zoals bij waardespreidingen kunnen we ook hier gebruik maken van een OF-uurlijst (ELKE_DAG) die de individuele dagen bevat:

Dergelijke OF-uurlijsten maken een verkorte schrijfwijze (in één lijn) mogelijk. We hoeven dus geen lijn per dag te schrijven.
Voor we plannen vergewissen we er ons ook nog van dat de minimumspreidingen worden meegenomen in de planning. We bekijken de opties (“Start | Opties | Roosteren | Algemene beperkingen”):
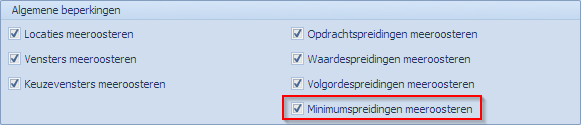
Vervolgens plannen we het geheel met dit als resultaat:
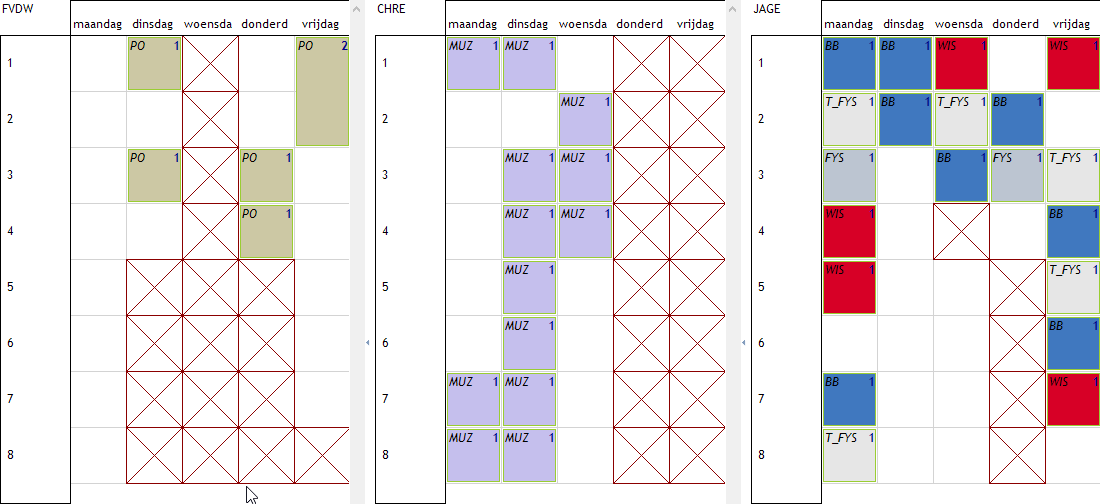
Elke leerkracht heeft nu minstens 2 uur les per dag of helemaal geen les.
Voorbeeld 2: voor 3 leerkrachten – Minimum 3 uur les per dag, of niets
Bekijken we het vorige rooster dan is het misschien wel mogelijk om minstens 3 uur les per dag te organiseren. We kunnen dat proberen. We maken een nieuwe regel aan (of passen de vorige aan) en maken enkel die regel actief die we wensen:

Na de planning zien we inderdaad dat het gelukt is, elke leerkacht heeft minstens 3 uur per dag les. De roosters zien er dus veel beter uit.
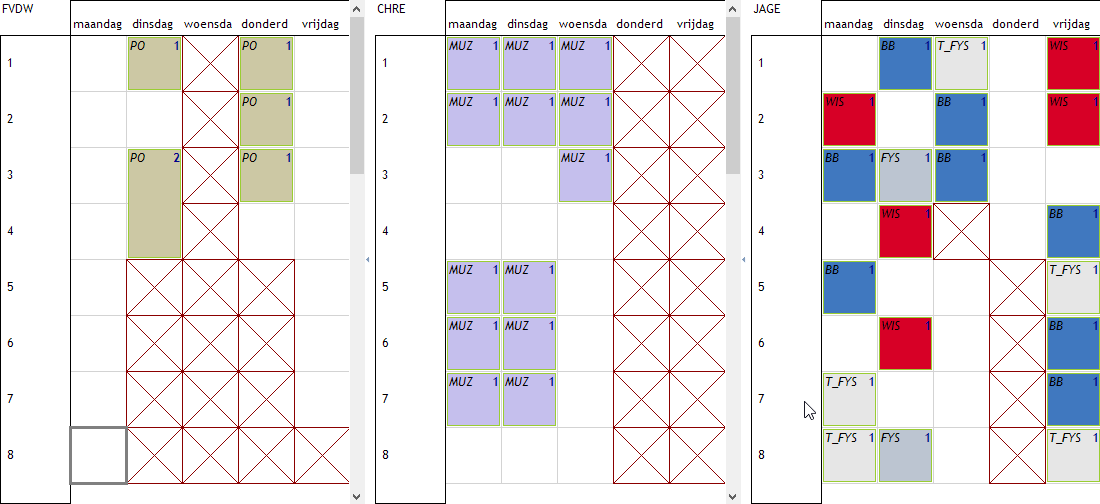
Voorbeeld 3: voor 3 leerkrachten – Minimum 4 uur les per dag, of niets. Is dit mogelijk?
Vraag is of we deze trend kunnen doortrekken. Kunnen we van die vorige Min 3 nu Min 4 maken? Er bestaat een kans dat dat lukt maar misschien niet voor elk van deze leerkrachten. Om dat na te gaan voor we aan de effectieve planning beginnen is het steeds nuttig om eerst eens een analyse te doen van de individuele leerkrachten. Als je elk van deze leerkrachten individueel zou roosteren, is het dan mogelijk om te eisen dat er minstens 4 uur les per dag gegeven wordt?
We maken eerst de nieuwe spreiding aan en zetten hem actief. De andere even op non-actief:

De eenvoudigste manier om de mogelijkheid uit te sluiten per individuele leerkracht is via “Analyseer opdrachten“.
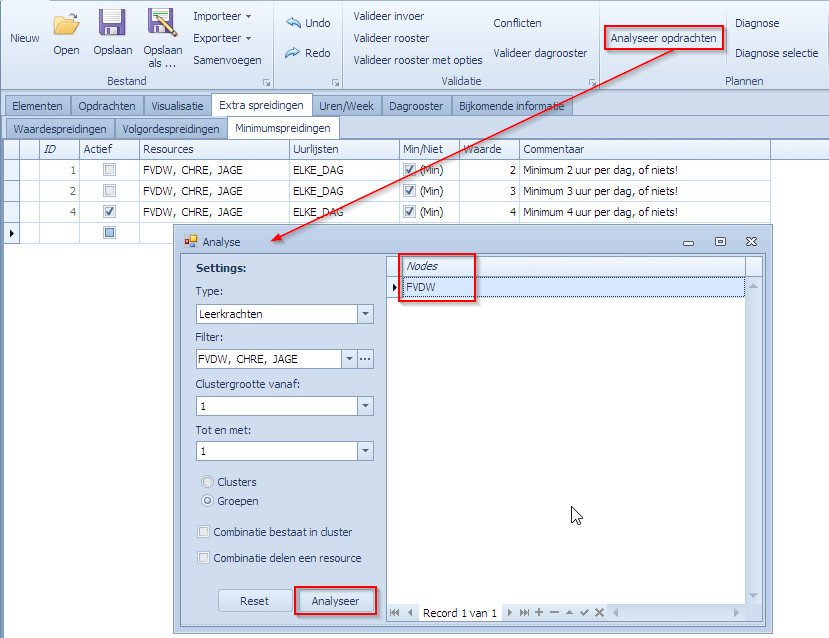
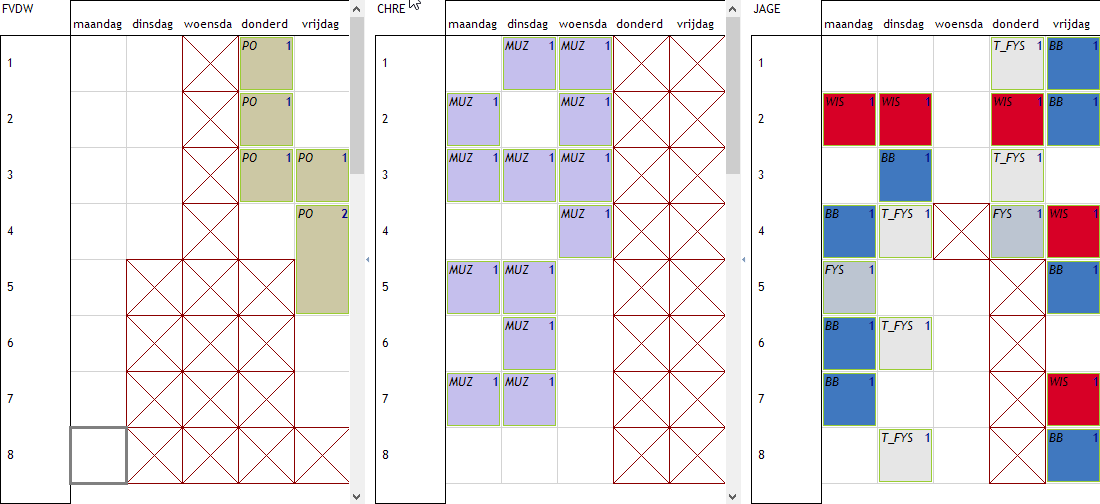
Deze analyse werd uitgevoerd en we zien dat er één leerkracht onmogelijk kan voldoen aan deze eis (in de context van alle instellingen en beperkingen). FVDW kan niet gepland worden met deze eis, de andere 2 wel. Dit wel echter niet zeggen dat als alles gecombineerd wordt dat het mogelijk blijft voor deze 2 leerkrachten, dat weten we pas als we de volledige planning doen. Dergelijke analyse is dus zeker nuttig om de flagrante problemen uit de planning te weren. We passen de spreidingen als volgt aan en kijken of dat een succes wordt:
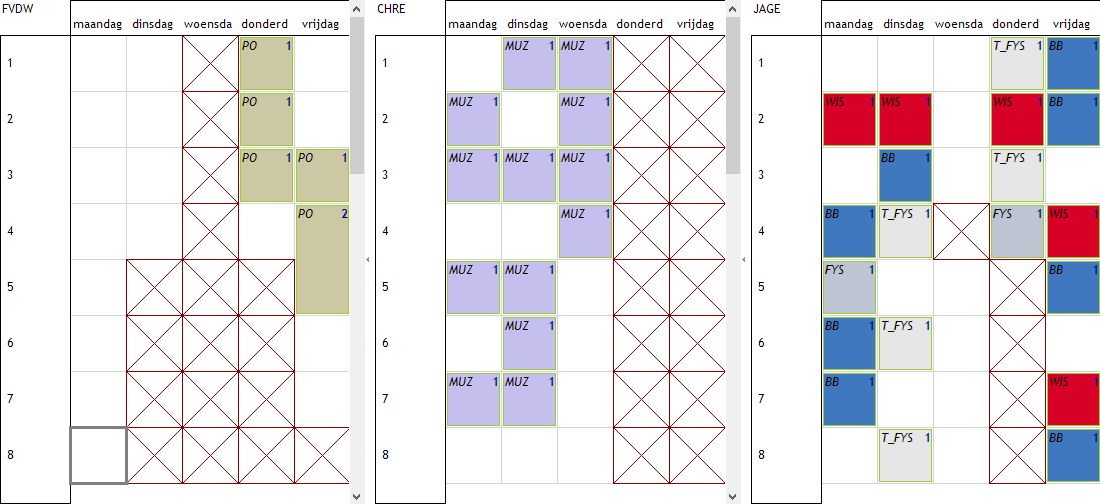
We plannen het geheel en zien dat het inderdaad succesvol is: CHRE en JAGE hebben nu minstens 4 uur les per dag en FVDW blijft op 3 uur per dag.
Voorbeeld 4: voor 3 leerkrachten – Niet 3 uur les per dag
Stel dat we de vreemde eis hebben om alles toe te laten behalve 3 uur les op een dag. Dat kan door volgende spreiding in te geven voor deze 3 leerkrachten. Merk op dat men via de checkbox kan switchen tussen Min en Niet.
- Aangevinkt = Min
- Uitgevinkt = Niet
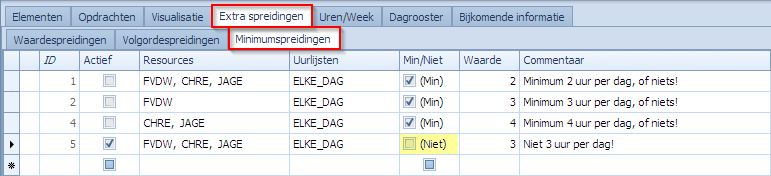
Plannen we met deze spreiding dan krijgen we dit. Inderdaad, geen van de 3 heeft op een dag 3 uur les. Het is steeds meer of minder dan 3.
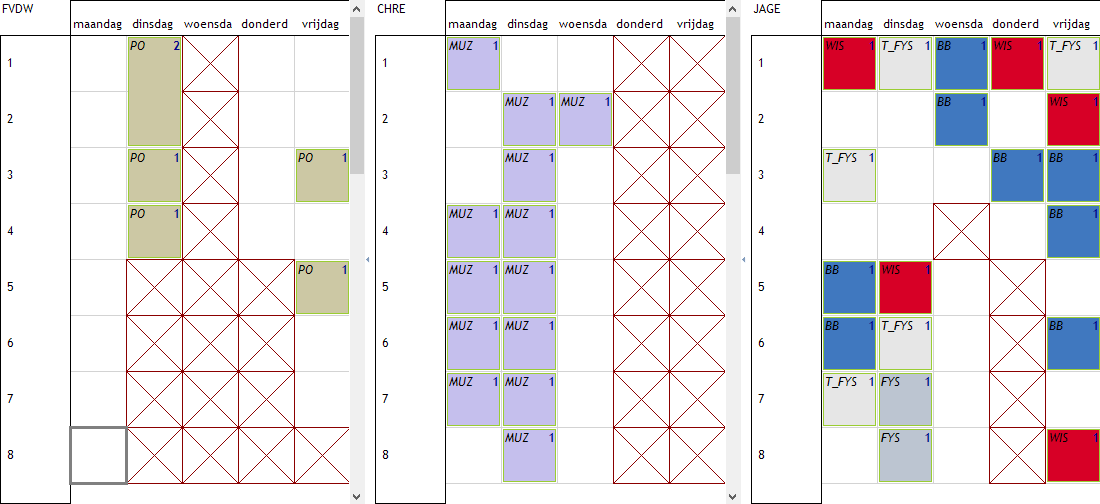
voorbeeld 5: een Min spreiding via een aantal Niet spreidingen
Zoals in de inleiding reeds aangehaald wordt een “Min x” spreiding door Mondriaan vertaald naar een aantal “Niet y” spreidingen. Om dat te illustreren maken we hier de Min spreidingen van voorbeeld 3 na via Niet spreidingen. In het tabblad ziet men nu 3 lijnen actief voor Niet spreidingen:
- Niet 1 op ELKE_DAG voor de 3 leerkrachten. Hiermee vermijden we dagen met 1 uur les.
- Niet 2 op ELKE_DAG voor de 3 leerkrachten. Hiermee vermijden we dagen met 2 uur les.
- Niet 2 op ELKE_DAG voor CHRE en JAGE. Hiermee vermijden we dagen met 3 uur les.
Dit komt dus overeen met de eis van voorbeeld 3.
- FVDW heeft hierdoor minimum 3 uur les per dag.
- CHRE en JAGE hebben minimum 4 uur les per dag.
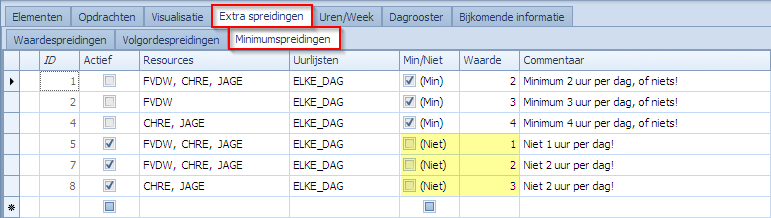
Na planning krijgen we een vergelijkbaar resultaat als in voorbeeld 3.
Resources waarvoor minimumspreidingen gedefinieerd kunnen worden
Minimumspreidingen kunnen voor volgende types resources gedefinieerd worden:
- Leerkrachten
- Klassen
- Lokalen
- Varia
Klassen en partitie-elementen
Klassen zijn een speciaal geval omdat klassen opgedeeld kunnen worden volgens bepaalde partities (Geslacht, Godsdienst, Keuze, …). Van zodra partitie-elementen in gebruik zijn in het rooster zullen minimumspreidingen gecontroleerd worden op het niveau van gecombineerde partitie-elementen. Dit is ook van toepassing voor waardespreidingen. Heb je bijvoorbeeld een klas 1A waarbij volgens de partitie Geslacht (meisje/jongen) gezwommen wordt en waarbij er bijvoorbeeld religie gevolgd wordt in 4 groepen (RKG/NCZ/ISL/PGD) dan ontstaan hierdoor 8 gecombineerde partitie-elementen voor 1A en voor elk van deze zal de minimumspreiding gelden. Elk van die 8 elementen representeert een uniek groepje leerlingen.
- 1A:meisje/RKG
- 1A:meisje/NCZ
- 1A:meisje/ISL
- 1A:meisje/PGD
- 1A:jongen/RKG
- 1A:jongen/NCZ
- 1A:jongen/ISL
- 1A:jongen/PGD
Men mag de minimumspreiding dan niet op het niveau van de volledige klas zien maar wel op niveau van deze groepjes.
Een voorbeeld: We vragen voor 1A min 2 per dag, of niets.
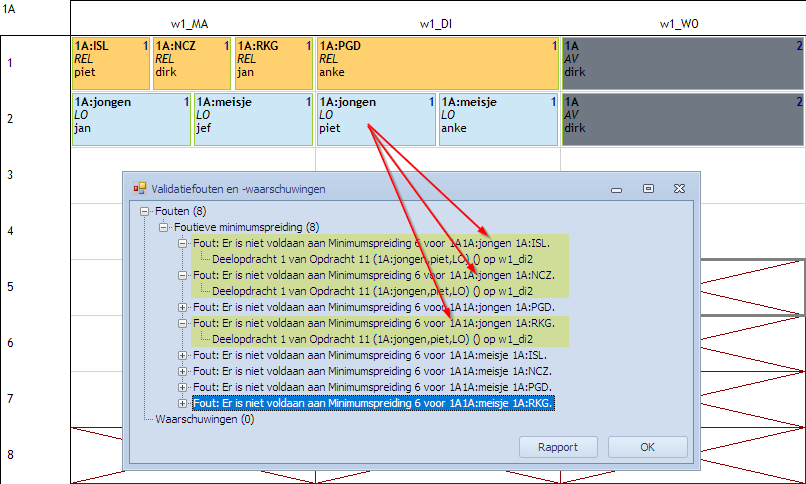
Volgende opdrachten zijn gepland in het rooster voor 1A. Als we dan vragen het rooster te valideren tegen deze Min 2 spreiding dan krijgen we 8 fouten te zien.
Voor dinsdag zien we dat jongens en meisjes LO hebben en dat ook het partitie-element PDG 1 uur les heeft. De min 2 spreiding wordt hier enkel gerespecteerd voor:
- 1A:jongen/PGD
- 1A:meisje/PGD
De 6 andere groepjes worden niet gerespecteerd. Bijvoorbeeld de jongens die RKG volgen, die hebben maar 1 uur les op dinsdag.
Voor maandag zien we dat jongens en meisjes LO hebben en dat ook de partitie-elementen ISL, NCZ en RKG 1 uur les hebben. Wat mankeert is PDG, zowel voor jongens als meisjes. Vandaar 2 groepjes waarvoor het niet gerespecteerd is.
Leerkrachten en wensen
Minimumspreidingen voor leerkrachten worden niet beïnvloed door leerkrachtwensen. Als men eist dat een leerkracht Min 3 uur per dag les heeft en hij heeft er maar 2 maar er staat ook eens wens van 4 uur dan telt die laatste dus niet mee. Minimumspreidingen hebben enkel effect op opdrachten die in het opdrachtentabblad gedefinieerd zijn.
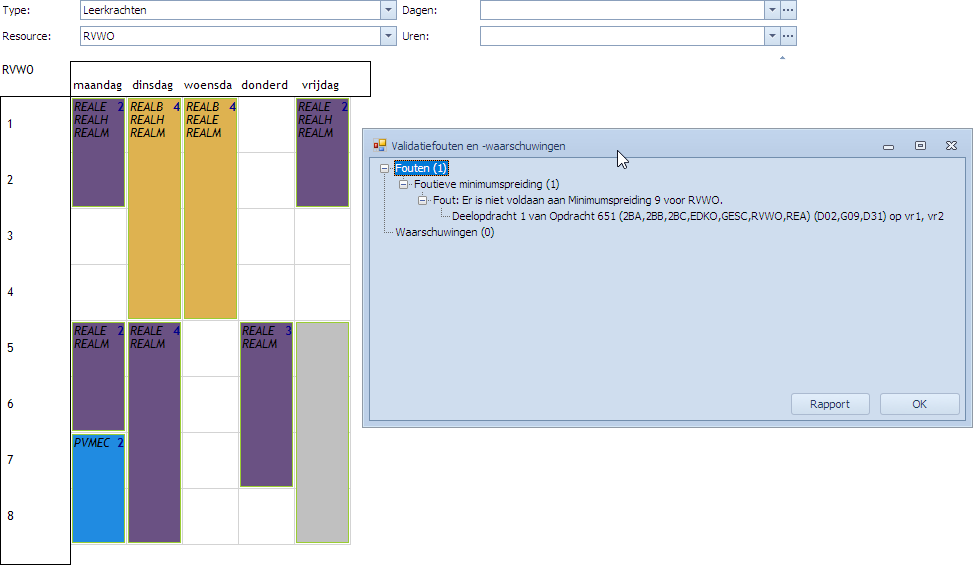
Voorbeeld van een spreiding: RVWO Min 3 uur les per dag.

Hier een voorbeeld waarbij niet aan deze Min 3 uur les op vrijdag voldaan is. Op vrijdag heeft RVWO 2 uur les en een wens van 4 uur in de namiddag. Die 4 uur telt dus niet mee. Doet men een “Valideer rooster” dan zal men exact zien waar het misloopt.
Doen we vervolgens een planning dan is dit wel een geldige situatie:
De MBE ondersteunt géén minimimspreidingen voor keuzeresources
Men kan in Mondriaan minimumspreidingen voor alle types resources (behalve vensters) definiëren maar van zodra een resource ook dienst doet als keuzeresource is er een probleem. Een resource is een keuzeresource van zodra ze ergens in een actieve opdracht deel uitmaakt van een keuzelijst (OF-takken). Van zodra een resource deel uitmaakt van een keuzelijst in een of meerdere opdrachten kan Mondriaan niet meer op voorhand bepalen hoeveel uur een resource effectief gebruikt gaat worden (na een volledige planning). Die kennis is achterliggend noodzakelijk opdat de MBE aan de minimumspreidingen correct kan voldoen tijdens het rekenen. Dus, de MBE moet weten wat de exacte bezetting gaat zijn en dat kan niet voor keuzeresources.
Mondriaan laat wel toe dat men een minimumspreiding definieert voor een keuzeresource maar zal een waarschuwing geven om aan te geven dat de MBE er géén rekening mee zal houden. Er is dus geen garantie dat er aan voldaan zal worden. Mondriaan kan zelf wél controleren of er aan voldaan is en ook daar de nodige Fouten/Waarschuwingen voor geven.
Voorbeeld van een waarschuwing: De groep LKR_MIN3 bevat alle leerkrachten waarvoor ze een Min 3 wensen af te dwingen.
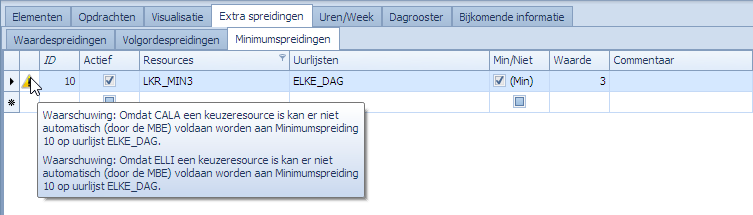
Ook de “Valideer invoer” geeft deze boodschappen:
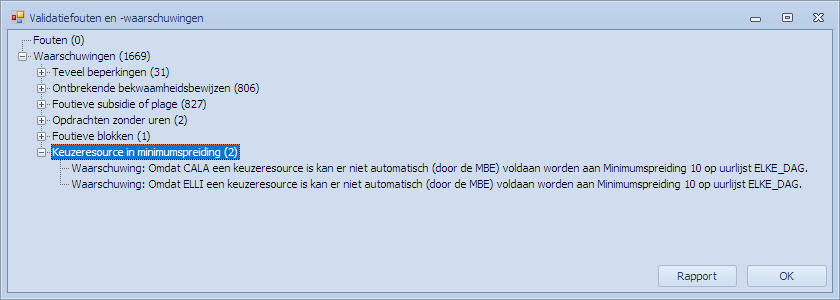
Zowel CALA als ELLI worden ergens als keuzeresource gebruikt en de waarschuwing geeft aan dat Mondriaan (MBE) er niet automatisch voor kan zorgen dat er aan die Min 3 voldaan zal worden. Doen we de planning met deze instellingen dan zou dit het resultaat kunnen zijn:
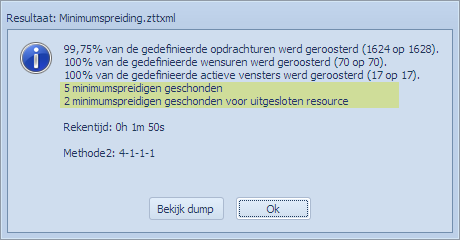
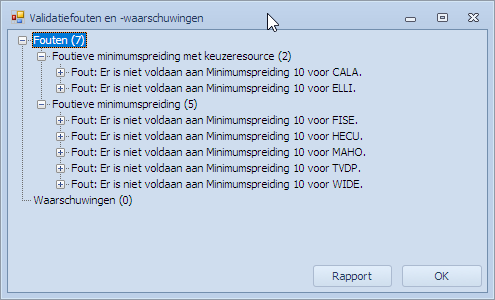
Er zijn 5 minimumspreidingen geschonden voor resources waarvoor Mondriaan (MBE) wel naar een oplossing zocht (niet aan kunnen voldoen in de huidige context en instellingen). Er zijn 2 minimumspreidingen geschonden voor uitgesloten resources. Dit zijn de 2 resources CALA en ELLI waarvoor Mondriaan sowieso geen oplossing kon zoeken omdat het keuzeresources zijn. Merk wel op dat het niet onmogelijk is dat er aan voldaan wordt. Door het toeval zou er wel aan voldaan kunnen zijn.
Doen we een “Valideer rooster” dan zien we ook het verschil tussen deze 5 en 2 geschonden minimumspreidingen:
Plan, Plan selectie en Analyse
Wanneer men een minimumspreiding definieert voor een resource dat moet dat steeds gezien worden in de context van ALLE actieve opdrachten waarin deze resource voorkomt. De gebruiker weet hoeveel lesopdrachten in het rooster van de resource terecht komen en de minimumspreiding moet in het licht daarvan bekeken worden.
Heeft BERT 20 uur les dan is het niet onmogelijk om te vragen dat BERT minstens 4 uur les per dag geeft of niets. Maar, stel dat we werken met een selectie aan opdrachten en dat er in die selectie maar 3 uur opgenomen zijn voor BERT. Als we die selectie plannen dan kan er nooit voldaan worden aan de eis dat BERT minstens 4 uur les geeft per dag omdat er maar 3 uur te plannen zijn. Dit is dus een onmogelijke situatie.
Om dergelijke onmogelijke situaties te voorkomen is de algemene regel om minimumspreidingen mee te nemen in de planning de volgende:
- Enkel indien ALLE actieve opdrachten voor resource X in de te plannen selectie zitten zullen ook de minimumspreidingen voor X opgenomen worden in de planning.
Voor de verschillende vormen van het automatisch plannen vertaalt zich dat in:
- Bij een normale volledige planning (Plan) is steeds aan die voorwaarde voldaan en zullen alle minimumspreidingen meegenomen worden.
- Bij het plannen van een selectie (Plan selectie) wordt per resource gekeken of al zijn actieve opdrachten in de selectie zitten en indien zo zullen ook zijn minimumspreidingen meegenomen worden.
- Bij een analyse (Analyseer opdrachten) wordt per te proberen combinatie, per resource gekeken of al zijn actieve opdrachten in de selectie zitten en indien zo zullen ook zijn minimumspreidingen meegenomen worden.
Opties in het optie-tabblad
Er zijn 2 opties beschikbaar voor minimumspreidingen:
In de sectie “Opties | Roosteren | Algemene beperkingen” staat de optie “Minimumspreidingen meeroosteren” standaard aan. Wenst men een planning te doen zonder deze spreidingen dan kan men deze optie uitvinken.
In de sectie “Opties | Manueel roosteren | Spreidingsconflicten” staat de optie “Extra Minimumspreidingsconflicten toestaan” standaard uit. Wenst men tijdens het manueel verschuiven van opdrachten geen rekening te houden met deze spreidingen kan men deze optie aanvinken.
Het grote verschil met waardespreidingen (achter de schermen)
In de inleiding werd al aangegeven dat een “Niet” waardespreiding niet helemaal hetzelfde is als een “Niet” minimumspreiding.
Het grote verschil tussen beide kan als volgt uitgelegd worden:
- “Niet” Waardespreiding: de opdrachten die onderhevig zijn aan deze spreiding kunnen tijdens de planning (door de MBE), in het zoekproces naar een volledige oplossing, op geen enkel moment deze spreidingsregel schenden. Op elk moment, onafhankelijk van hoe gevuld het rooster is, er zal steeds en altijd voldaan zijn aan deze spreiding.
- “Niet” Minimumspreiding: de opdrachten die onderhevig zijn aan deze spreiding kunnen tijdens de planning (door de MBE), in het zoekproces naar een volledige oplossing, op elk moment deze spreidingsregel schenden, behalve als de planning volledig is. Op elk moment, onafhankelijk van hoe gevuld het onvolledig rooster is, kan er aan de spreiding voldaan zijn of niet.
Dat verschil is essentieel. Denk bijvoorbeeld aan de “Min 3” minimumspreiding op elke dag. Hiervan hebben we gezegd dat ze achter de schermen vertaald wordt naar volgende minimumspreidingen:
- Niet 1 op elke dag
- Niet 2 op elke dag
Stel dat op elk moment in de opbouw naar een volledig rooster op elk moment aan beide beperkingen moet voldaan worden dan wordt het onmogelijk om het rooster op te bouwen:
- Zetten we het eerste uur in het rooster dan zou dat niet gaan vanwege Niet 1.
- Zetten we het tweede uur in het rooster op dezelfde dag dan zou dat niet gaan vanwege Niet 2
Vandaar dat we voor minimumspreidingen een techniek voorzien hebben die wel toelaat dat tijdens de opbouw de regels geschonden worden. Het eindresultaat is uiteraard dat aan de beperking voldaan wordt.
De basis van de minimumspreiding is deze speciale vorm (tijdelijk schendbaar) van “Niet” spreiding. En deze speciale “Niet” spreiding wordt op haar beurt achter de schermen bekomen door een combinatie van
- een “Niet” waardespreiding.
- dummy opdrachten die het rooster van de resource in kwestie volledig opvullen
Dus, via een combinatie van de klassieke “Niet” waardespreiding en een set dummy opdrachten die het rooster volledig vult kunnen we het beoogde effect bekomen. Het tijdelijk niet in het rooster zitten van dummy opdrachten geeft de MBE ruimte om tijdelijk niet aan de spreiding te voldoen. De dummy opdrachten genereren ook de nodige turbulentie tijdens het roosteren omdat ze zonder meer conflicteren met de gewone lesopdrachten.
Dit systeem waarbij het rooster van de resource volledig gevuld wordt met dummy opdrachten is de reden dat dit systeem niet werkt voor keuzeresources. De MBE moet namelijk het exacte aantal dummy opdrachten op voorhand kennen en dat kan enkel als men ook het aantal te plannen lesopdrachten exact kent voor die resource.
Bij het gebruik van minimumspreidingen ontstaan extra dummy opdrachten voor de MBE
De dummy opdrachten waarvan sprake zijn niet zichtbaar voor de gebruiker in Mondriaan. Enkel wanneer een planning opgestart wordt zal men tijdens het rekenen van de MBE zien dat er plots met meer opdrachten gerekend wordt dan normaal. Gaat het bijvoorbeeld om een minimumspreiding voor één leerkracht die 20 uur les heeft in een rooster van 50 uur, dan zal men zien dat er plots een 30-tal extra opdrachten verwerkt worden. Gaat men minimumspreidingen voor alle leerkrachten invoeren dan kan het goed zijn dat men plots het dubbel aantal of zelfs meer ziet verschijnen tijdens het rekenen.
Zeker voor minimumspreidingen in multiweeksystemen kan het aantal dummy opdrachten al snel erg hard oplopen.
Al deze extra opdrachten zorgen uiteraard ook voor een verzwaring van het systeem en kan de rekentijd hierdoor soms erg oplopen.
Nog enkele tips over minimumspreidingen
Meest gebruikte toepassing
De oorsprong van deze spreiding ligt in de vraag van vele scholen om op een automatische manier geïsoleerde uren voor resources te vermijden. In theorie is dat ook mogelijk zonder minimumspreidingen maar dan vraagt dat erg veel administratie in Mondriaan en die is lastig te onderhouden als de opdrachten wijzigen. Die administratie wordt door de minimumspreidingen achter de schermen beheerd.
De grootste toepassing van deze spreiding is zeker het verbeteren van de kwaliteit van leerkrachtroosters. De combinatie met wensen is geen probleem. Ook het gebruik van (automatische) optimalisatie van leerkrachtroosters blijft mogelijk maar door het gebruik van deze spreidingen zal de noodzaak voor die optimalisatie veel minder zijn.
Naast deze toepassing hebben we ervoor gezorgd dat het ook bruikbaar is voor andere types resources en redenen.
Gebruik de analysetool om de haalbaarheid te evalueren
Het is nu erg gemakkelijk om bijvoorbeeld voor alle leerkrachten in de school te eisen dat ze bijvoorbeeld minstens 2 uur les per dag (of halve dag, …) geven of niets. Dergelijke eenvoudige eis zorgt wel meteen voor een grote complexiteitsverhoging waarvan men niet weet of het kan lukken. Als men ziet dat de MBE er plots erg lang over begint te rekenen is het zeer nuttig om even te kijken of dergelijke eis al voldaan kan worden als men de resources individueel gaat plannen. Dat kan men perfect doen door even de “Analyseer opdrachten” te draaien voor bijvoorbeeld elke leerkracht individueel. Ziet men dat daar bepaalde leerkrachten onmogelijk kunnen voldoen aan die eis dan haalt men die best eerst uit de spreiding alvorens te plannen voor het geheel.
Men kan uiteraard ook 2 per 2 resources analyseren of eender welke andere combinatie. De technieken zijn uitgelegd in “Analyseren van opdrachten“. Meer specifiek kan men eens kijken naar “Analyseer individueel“.
Bij rekenen met Methode2 kan de optie M2b nuttig zijn
Als er veel minimumspreidingen in het spel zijn (zoals bij de eis voor alle leerkrachten …) is het nuttig gebleken om de optie M2b aan te vinken voor het plannen. De b-versie van Methode2 geeft dat vaak sneller resultaat dan de a-versie. Voor meer informatie zie “Opties | Engine | Roosteren“.
Gebruik deze spreiding verstandig en met mate
Dit type spreiding moet men enkel gebruiken als het echt nodig is. Een beperking die evengoed via een waardespreiding bereikt kan worden doet men veel beter via een waardespreiding. Denk bijvoorbeeld aan het veelvuldig gebruik van een “Niet” waardespreiding voor het regelen van verplaatsingen tussen locaties. Dit is het soort probleem waarbij de MBE de oplossing kan bereiken door de roosters geleidelijk aan te vullen. Aan de spreiding moet op elk moment tijdens de planning voldaan zijn. Hiervoor blijft men uiteraard waardespreidingen gebruiken.
Heb je nood aan een “Min x” spreiding voor een resource, gebruik dan sowieso de minimumspreiding. heb je nood aan een “Niet x” spreiding voor een resource, denk dan eerst aan de waardespreiding. Als een “Niet x” spreiding steeds moet of mag gelden, onafhankelijk hoe ver het rooster gevuld is, dan is een waardespreiding waarschijnlijk goed. In het andere geval, waarbij we onderweg wel schending van de spreiding nodig hebben is een “Niet” minimumspreiding de oplossing.