Analyseren van opdrachten
Het plannen van een rooster gaat vaak gepaard met het onderzoeken van strijdige stelsels van opdrachten en beperkingen, of meer algemeen, van knelpunten in het rooster waardoor een oplossing erg moeilijk wordt. Als er niet genoeg “zuurstof” in de opdrachten en beperkingen zit, kan het soms zoeken zijn naar een speld in een hooiberg. We moeten niet alleen aandacht besteden aan strijdige stelsels, maar ook aan knelpunten die het roosteren erg bemoeilijken.
De MBE kan strijdige stelsels niet zelf oplossen en dit leidt vaak tot frustratie bij de gebruiker omdat deze niet weet waar het probleem vandaan komt. Mondriaan heeft wel een aantal tools die kunnen helpen bij het opsporen van strijdigheden in het systeem. Plant men alle opdrachten en komt de MBE niet tot een oplossing (opdrachten falen), of niet snel genoeg, dan is de vraag waaraan dit ligt niet makkelijk te beantwoorden, omdat er vaak erg veel opdrachten en beperkingen in het spel zijn.
De kunst bij het opsporen van dergelijke strijdigheden of knelpunten is het inzoomen op een zo klein mogelijke set van opdrachten en beperkingen waarbinnen het probleem zich voordoet. Indien men een bepaald vermoeden heeft vanwaar het probleem komt dan kan men met volgende tools al een eind komen:
- Plan Selectie: men selecteert en plant een deel van de opdrachten om te zien of het probleem zich dan ook stelt.
- Roosteropties: via de besproken roosteropties (Opties | Roosteren) kan men allerhande beperkingen globaal uitschakelen om te zien of de problemen zich dan nog voordoen.
- Combinaties van beide technieken.
Via “Plan Selectie” kan men beginnen zoeken naar de kleinste set van opdrachten/beperkingen waarvoor het probleem zich voordoet om vervolgens de nodige relaxaties te doen in de opdrachten en beperkingen. Het zoeken naar die set is soms een lastig probleem op zich.
Mondriaan biedt een extra mogelijkheid om op een automatische manier naar die set van opdrachten te zoeken die problemen veroorzaken binnen de context van de roosteropties en MBE opties. De tool die hiervoor bestaat, vindt men in de toolbar onder “Start | Plannen | Analyseer Opdrachten“.
Via deze tool kan de gebruiker de grenzen bepalen waarbinnen Mondriaan combinaties van opdrachten gaat onderzoeken (=proberen te plannen). Het onderzoeken van de deelverzamelingen gebeurt door telkens die deelverzameling aan de MBE aan te bieden en te zien of er binnen de context van de Rooster en MBE Opties tot een oplossing gekomen wordt. Alle deelverzamelingen waarvoor dit niet lukt, worden dan aan de gebruiker getoond zodat men op basis van deze strijdige deelverzamelingen verder kan inzoomen op het probleem.
Inhoud
- Analyseren is (veel) deelverzamelingen van opdrachten afzonderlijk proberen
- Context waarbinnen de analyse gebeurt
- Openen van de analysetool
- Overlopen van enkele “Analyseer opdracht” technieken
- Opzoeken van knelpunten door de MBE minder zoekvrijheid te geven
- Een gefaalde combinatie gebruiken als filter voor bijvoorbeeld Plan Selectie
- Dubbelklik op een gefaalde combinatie toont de gefaalde opdrachten
- Minder combinaties proberen door de “Cluster”-techniek
- Teveel combinaties analyseren
- Analyse stoppen na eerst gefaalde groep
- Analyseer Individueel
- Behouden van de gegevens van een Analyseer Opdrachten
- Locatie van tekstbestanden die de MBE aanmaakt bij Analyseer opdrachten
- Extra analysebestanden met statistieken over de uitgevoerde analyse
Analyseren is (veel) deelverzamelingen van opdrachten afzonderlijk proberen
De manier waarop we via deze tool problemen trachten op te sporen is door steeds andere combinaties van opdrachten aan te bieden aan de MBE. Als je maar alle mogelijke combinaties van opdrachten naar de MBE stuurt, zal er uiteindelijk wel de kleinste combinatie uitkomen die strijdig is of een knelpunt vormt. En daar zit nu het probleem, we kunnen onmogelijk alle combinaties van opdrachten aanbieden omdat dat veel te lang zou duren. Om een idee te geven van wat het bijvoorbeeld zou betekenen indien we in totaal 10 opdrachten zouden hebben dan kunnen we volgende combinaties van opdrachten naar de MBE sturen:
- 1 opdracht sturen: 10 combinaties (1 opdracht uit 10 opdrachten)
- 2 opdrachten sturen: 45 combinaties (2 opdrachten uit 10 opdrachten)
- 3 opdrachten sturen: 120 combinaties (3 opdrachten uit 10 opdrachten)
- 4 opdrachten sturen: 210 combinaties (4 opdrachten uit 10 opdrachten)
- 5 opdrachten sturen: 252 combinaties (5 opdrachten uit 10 opdrachten)
- 6 opdrachten sturen: 210 combinaties (6 opdrachten uit 10 opdrachten)
- 7 opdrachten sturen: 120 combinaties (7 opdrachten uit 10 opdrachten)
- 8 opdrachten sturen: 45 combinaties (8 opdrachten uit 10 opdrachten)
- 9 opdrachten sturen: 10 combinaties (9 opdrachten uit 10 opdrachten)
- 10 opdrachten sturen: 1 combinaties (10 opdrachten uit 10 opdrachten)
Dat zijn opgeteld 1.023 combinaties voor maar 10 opdrachten. Voor 11 opdrachten zouden dat er al 2.047 zijn. Als men enkele duizenden opdrachten heeft, kan men zich voorstellen dat alles uittesten absoluut geen optie is.
Er moeten dus keuzes gemaakt worden over welke beperkte combinaties we aan de MBE zullen aanbieden om een analyse van de opdrachten te doen. Een eerste oplossing om de combinaties te beperken is door met combinaties van elementen te werken in plaats van met combinaties van individuele opdrachten.
Combinaties van elementen maken i.p.v. van combinaties van opdrachten
Een eerste manier om combinaties te beperken vertrekt niet van een combinatie van individuele opdrachten, maar combineert elementen en selecteert voor die combinaties van elementen de overeenkomstige opdrachten. Meestal ontstaat een strijdig stelsel toch vanuit een resource waar teveel beperkingen voor bestaan indien we die resource plannen in combinatie met de opdrachten van één of meerdere andere resources. Dus, selecteer je bijvoorbeeld alle opdrachten van klas 1A (bv 25) en plan je die, dan kan het zijn dat het rooster van 1A perfect opgelost wordt. Hetzelfde kan gelden voor de opdrachten van een klas 1B (bv 25). Neem je vervolgens alle opdrachten van 1A en 1B samen (bv 40 omdat ze gedeeltelijk samen zitten en dus gemeenschappelijke opdrachten hebben) dan kan het zijn dat het plots niet meer lukt. Het feit dat 1A en 1B samen een knelpunt vormen, is erg nuttige informatie. Op basis hiervan kan de gebruiker gemakkelijk op zoek gaan naar de reden van het knelpunt, omdat het over een beperkte set aan opdrachten gaat (40 in dit voorbeeld). Op basis van die 40 kan men dan verder inzoomen tot men het probleem ofwel in de opdrachten, ofwel in de spreidingen of andere beperkingen gevonden heeft.
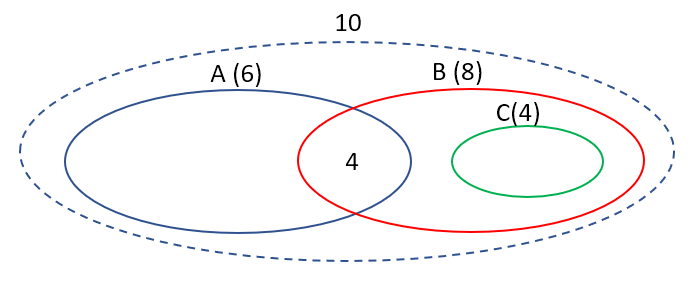
Stel dat we 10 opdrachten hebben voor de elementen A, B en C. Stel dat we dan volgende verdeling hebben over die 10 opdrachten:
- A zit in 6 van de 10 opdrachten
- B zit in 8 van de 10 opdrachten
- C zit in 4 van de 10 opdrachten
A, B, en C zullen in die 10 opdrachten in bepaalde combinaties samenzitten. Bijvoorbeeld:
- A en B samen in 4 van de 10 opdrachten
- B en C samen in 4 van de 10 opdrachten
- A en C niet samen
Als we nu alle combinaties van elementen gaan maken om te analyseren komen we bijvoorbeeld tot volgende beperkte set van 7 combinaties:
- (A): 6 opdrachten
- (B): 8 opdrachten
- (C): 4 opdrachten
- (A, B): 10 opdrachten (6 + 8 – 4 overlap)
- (A, C): 10 opdrachten (6 + 4)
- (B, C): 8 opdrachten (8 + 4 – 4 overlap)
- (A, B, C): 10 opdrachten
Elk van deze 7 combinaties kan naar de MBE gestuurd worden om te plannen. Van zodra een combinatie niet gepland kon worden, kan de gebruiker hier verder op inzoomen. De MBE hoeft ook niet alle combinaties te proberen. Als bijvoorbeeld de combinatie (A) faalt, dan heeft het verder geen zin om de combinatie (A,B) te testen. Of als (A,C) faalt heeft het geen zin om (A,B,C) te testen. Dus, tijdens de analyse kan Mondriaan beslissen om een grotere combinatie niet meer te proberen omdat een deelverzameling ervan al faalde.
Door combinaties van elementen te nemen, reduceren we het aantal te testen opdrachtcombinaties al drastisch, maar er blijven nog veel te veel elementencombinaties mogelijk. Om het aantal te testen elementencombinaties verder te verkleinen biedt Mondriaan aan de gebruiker een aantal opties aan. Via deze opties heeft men invloed op volgende vragen:
- Welke elementen kunnen in combinaties voorkomen?
- Hoe groot mogen de combinaties van elementen zijn?
- Welke types van elementen mogen samen in een combinatie voorkomen?
- Kunnen we nog extra voorwaarden stellen opdat een combinatie weerhouden wordt?
Gosso modo delen we de methodes in volgens de Groepen methode en de Cluster methode. Voor elk van deze 2 methodes leggen we uit hoe deze 4 vragen beantwoord worden.
Volgende tabel geeft een overzicht van de mogelijkheden:
| Groepen-methode | Cluster-methode | |
| 1. Elementen die kunnen voorkomen in combinaties? | Opsomming van elementen (Filter veld) door gebruiker. Dit zijn de enige elementen die in combinaties kunnen voorkomen. | Opsomming van elementen (Filter veld) door gebruiker. Dit is enkel het startpunt. Via de cluster-detectie-methode worden hier nog extra elementen aan toegevoegd. (zie verder). |
| 2. Grootte van de elementencombinaties? | Men geeft de minimale (Clustergrootte vanaf veld) en maximale grootte (Tot en met veld) op van combinaties de getest mogen worden. | Zelfde manier |
| 3. Types van elementen die gecombineerd mogen worden? | Alle elementen kunnen met elkaar gecombineerd worden, onafhankelijk van het type. Een klas samen met een lokaal kan dus perfect. | Per combinatie zijn de types van de elementen gelijk. Een klas met een lokaal kan dus niet. Meer nog, de enige types waarvoor combinaties gemaakt worden zijn ook types die in het Filter voorkomen. |
| 4. Extra beperkingen op de combinaties? |
keuze: Combinatie bestaat in Cluster? veld (zie verder) keuze: Combinatie delen een resource? veld (zie verder) |
Enkel combinaties die in een getypeerde cluster bestaan worden weerhouden. (zie verder) |
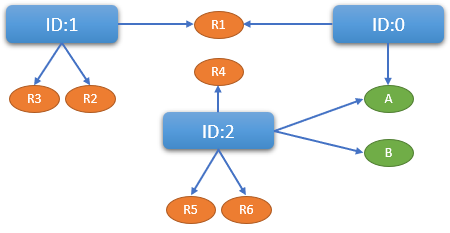
Een aantal concepten uit deze tabel moeten nog uitgelegd worden. We zullen hiervoor af en toe gebruik maken van dit kleine artificiële voorbeeld met 3 opdrachten (ID’s 0, 1, 2). We hebben de elementen A, B, R1, …, R6. We hebben 2 types elementen: klassen en leerkrachten.
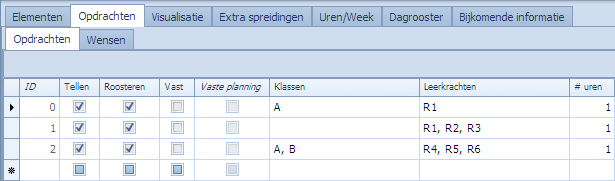
Rechts een visuele voorstelling die kan helpen bij het begrijpen van de voorbeelden. |
 |
Stel dat we A, R1, R2 opgeven als Filter elementen voor de analyse. We stellen ook dat we combinaties van 1 of 2 elementen wensen door te geven aan de MBE om te testen (plannen). Laat ons met die instelling de methoden Groepen en Clusters bekijken.
Groepen-methode
Combinaties van 1 element en combinaties van 2 elementen waarbij de types door elkaar gebruikt mogen worden. Dat levert volgende mogelijkheden op waarbij we meteen ook weergeven welke opdrachten (ID’s) geselecteerd zullen worden voor elk van de combinaties:
Combinaties van 1:
- (A) ⇒ 0, 2
- (R1) ⇒ 0, 1
- (R2) ⇒ 1
Combinaties van 2:
- (A, R1) ⇒ 0, 1, 2
- (A, R2) ⇒ 0, 1, 2
- (R1, R2) ⇒ 0, 1
Zonder verdere beperkingen zullen dit de 6 combinaties zijn die we een voor een naar de MBE sturen. Merk op dat we vanwege het kleine voorbeeld we vaak dezelfde opdrachten zullen selecteren. De eerste 2 combinaties leveren inderdaad exact dezelfde opdrachten op.
Cluster-methode
Bij de cluster methode worden de opgegeven filterelementen niet rechtstreeks gebruikt om er combinaties van 2 van te maken. Hier komen we op de vermeldde cluster-detectie-methode om de te gebruiken elementen te bepalen en om te bepalen welke combinaties er gemaakt mogen worden.
Wat is een Cluster in deze context? Als je een opdracht bekijkt, zijn de clusters de groepjes elementen van die opdracht die van hetzelfde type zijn. We kunnen in de 3 opdrachten volgende clusters onderscheiden:
- ID0: (A) en (R1)
- ID1: (R1, R2, R3)
- ID2: (A, B) en (R4, R5, R6)
De cluster-detectie-methode start van de elementen uit de filter (A, R1, R2). De methode zoekt eerst alle opdrachten die iets met de elementen in de filter te maken hebben. In dit geval zijn dat alle opdrachten. Van deze nemen we alle clusters:
- (A), (R1), (R1, R2, R3), (A, B), (R4, R5, R6)
Enkel combinaties met elementen uit deze clusters zijn mogelijk. Sterker nog, als je een combinatie van 2 elementen maakt mag dat enkel indien ze ook samen in een cluster zitten. Dit slaat op de impliciete extra beperking die geldt voor de Cluster methode (vraag 4: Extra beperkingen op de combinaties?). Passen we die logica toe dan krijgen we volgende combinaties van 1 en 2:
Combinaties van 1:
- (A) ⇒ 0, 2
- (B) ⇒ 2
- (R1) ⇒ 0, 1
- (R2) ⇒ 1
- (R3) ⇒ 1
- (R4) ⇒ 2
- (R5) ⇒ 2
- (R6) ⇒ 2
Combinaties van 2:
- (A, B) ⇒ 0, 2
- (R1, R2) ⇒ 0, 1
- (R1, R3) ⇒ 0, 1
- (R2, R3) ⇒ 1
- (R4, R5) ⇒ 2
- (R4, R6) ⇒ 2
- (R5, R6) ⇒ 2
Wat bijvoorbeeld niet kan is (A, R1) omdat ze niet in 1 cluster kunnen zitten, omdat ze niet van hetzelfde type zijn. Wat ook niet kan is (R1, R4) omdat ze niet in dezelfde cluster zitten.
Opnieuw de opmerking dat we vanwege dit kleine voorbeeld voor meerdere combinaties dezelfde opdrachten selecteren.
Men ziet nu duidelijk het verschil tussen de elementen die gebruikt worden en de manier waarop de combinaties samengesteld worden tussen beide methodes.
Wat met cluster-detectie-methode in het geval dat er keuzeresources zijn? Stel dat leerkrachten R1, R2, R3 in opdracht ID1 keuzeresources zouden zijn. In dat geval moet de opdracht een van de resources kiezen en kunnen ze niet samen geplaatst worden. Dat heeft ook een belangrijke impact op de clusters die bekeken worden. We zouden dan volgende clusters krijgen:
- ID0: (A) en (R1)
- ID1: (R1) en (R2) en (R3)
- ID2: (A, B) en (R4, R5, R6)
Dit zou nu geen invloed hebben op de combinaties van 1 maar wel op die van 2. De resulterende combinaties van 2 zouden de volgende zijn:
- (A, B) ⇒ 0, 2
- (R4, R5) ⇒ 2
- (R4, R6) ⇒ 2
- (R5, R6) ⇒ 2
Stel dat er 2 groepen van keuzelokalen zouden zijn in 1 opdracht, eentje van 2 en eentje van 3 lokalen. In dat geval willen we dus 2 lokalen laten kiezen. Bijvoorbeeld keuze uit (L1, L2) samen met een keuze uit (L2, L3, L4) in dezelfde opdracht (met bv 1 lokaal in beide keuzegroepen). Op dat moment worden de clusters gevormd door enkel de mogelijke combinaties:
- (L1, L2) en (L1, L3) en (L1, L4) en (L2, L3) en (L2, L4)
Extra beperkingen op de combinaties voor de Groepen methode
Voor vraag 4 in het geval van Groepen hebben we nog 2 beperkende voorwaarden die nog uitgelegd moeten worden. Zonder die extra voorwaarden laten we alle gevonden combinaties toe. Elk van deze beperkende voorwaarden gaat uit van combinaties die minstens grootte 2 hebben. De combinaties met 1 element vallen er dan sowieso uit.
Volgende extra beperkingen zijn mogelijk:
Combinatie bestaat in cluster: De combinatie wordt enkel weerhouden als ze effectief in minstens één opdracht voorkomt (met cluster bedoelen we hier alle elementen uit de opdracht, ongeacht hun type). Door deze beperking op te leggen is men zeker dat de elementen in de combinatie elkaar beïnvloeden tijdens het plannen. Ze worden samen door minstens een opdracht in het rooster geplaatst. Dan weet je dat er een koppeling is en het dus de moeite is om ze samen te testen.
- (A, R1) komt voor in ID0.
- (A, R2) komt nergens voor en zal dus niet weerhouden worden.
Passen we deze regel toe op de combinaties die we eerder bepaalt hebben voor Groepen dan resulteert dit in:
Combinaties van 1:
(A)(R1)(R2)
Combinaties van 2:
- (A, R1) ⇒ 0, 1, 2
(A, R2)- (R1, R2) ⇒ 0, 1
Combinatie delen een resource: Een combinatie wordt weerhouden indien er een willekeurige (niet-keuze) element bestaat (verschillend van de elementen in de combinatie) die via willekeurige opdrachten (meer dan 1) met elk van de elementen uit de combinatie verbonden is. Ook door deze beperking op te leggen is men zeker van een koppeling tussen de elementen van de combinatie. De koppeling is minder direct dan bij “De combinatie moet in een opdracht bestaan”, het is een aan de combinatie extern element dat een koppeling tussen de elementen van de combinatie veroorzaakt.
Passen we deze regel toe op de combinaties die we eerder bepaald hebben voor Groepen dan resulteert dit in:
Combinaties van 1:
(A)(R1)(R2)
Combinaties van 2:
(A, R1)- (A, R2) ⇒ 0, 1, 2
(R1, R2)
Beide voorwaarden samen aanvinken:
Indien men beide opties samen kiest dan krijgt men de unie van beide keuzes. Je gaat dan zowel de sterke als de zwakkere koppelingen tussen de elementen van de combinatie aanvaarden als reden om ze mee te nemen.
De resulterende combinaties zijn dan de volgende:
Combinaties van 1:
(A)(R1)(R2)
Combinaties van 2:
- (A, R1) ⇒ 0, 1, 2
- (A, R2) ⇒ 0, 1, 2
- (R1, R2) ⇒ 0, 1
Nog een voorbeeld om de verschillen aan te tonen
We hernemen het voorbeeld en gebruiken nu volgende elementen uit de 3 opdrachten in de filter: A, B, R1, R2, R4, R5. We kiezen combinaties van grootte 1 tot 2 en we bekijken dit voor volgende 5 instellingen:
- Groepen Methode: Geen bijkomende voorwaarden
- Groepen Methode: Combinatie bestaat in opdracht
- Groepen Methode: Combinatie delen een resource
- Groepen Methode: Combinatie bestaat in opdracht of Combinatie delen een resource
- Cluster Methode
We tonen nogmaals de 3 eenvoudige opdrachten en al een preview van het optiescherm waarmee we de analyseparameters bepalen:
 |
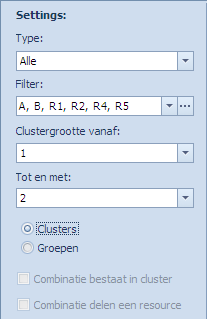 |
Afhankelijk van de 5 instellingen toont volgende tabel de resulterende combinaties die naar de MBE gestuurd zullen worden.
| 1. Groepen: Geen beperking | 2. Groepen: Bestaat in opdracht | 3. Groepen: Delen een resource | 4. Groepen: Beide beperkingen | 5. Cluster |
|
|
|
|
Anders gekleurde zijn combinaties die niet kunnen voorkomen bij Groepen. |
|
|
|
|
|
Welke methode gebruiken?
Strikte regels kunnen niet gegeven worden maar deze inzichten kunnen wel helpen in de keuzes:
- Groepen Methode: Geen bijkomende voorwaarden: Het aantal combinaties neemt exponentieel toe met het aantal elementen in de filter en met de grootte van de gevraagde combinaties. Men zal al snel merken wanneer dit niet langer houdbaar is. Voor kleine combinaties (bv max 2) is het zeker nog doenbaar met niet teveel elementen. Heeft men bijvoorbeeld 100 elementen dan heeft men met combinaties van 2 toch al snel 4.950 combinaties van 2. Heeft men 100 elementen en vraagt men combinaties van 3 dan zijn dat er al 161.700 combinaties van 3 die een voor een naar de MBE gestuurd worden. Dit is niet doenbaar. Deze methode houdt dan ook weinig rekening met de effectieve verbanden tussen de elementen in de combinatie.
- Groepen Methode: Combinatie bestaat in opdracht: Door te eisen dat de elementen van de combinatie ook samen in minstens 1 opdracht voorkomen gaat men het aantal combinaties uit 1 al sterk verminderen. Men limiteert de combinaties door een sterke vorm van koppeling te eisen tussen de elementen.
- Groepen Methode: Combinatie delen een resource: Door te eisen dat alle elementen van de combinatie door minstens een ander extern element beperkt worden gaat men het aantal combinaties uit 1 sterk verminderen. We kunnen dit een zwakke koppeling tussen de elementen noemen. Echter, ook dergelijke koppelingen kunnen de plaatsing van het geheel onmogelijk maken. Men limiteert de combinaties door een zwakke koppeling te eisen tussen de elementen.
- Groepen Methode: Combinatie bestaat in opdracht of Combinatie delen een resource: Hier gaat men meteen met de sterke en de zwakke koppelingen tegelijk rekening houden. Geeft uiteindelijk hetzelfde resultaat als ze apart proberen.
- Cluster Methode: Dit is de meest complexe methode met als doel zo verstandig mogelijk zo weinig mogelijk combinaties uit te proberen. Hier wordt de harde koppeling tussen de elementen van de te testen combinaties impliciet afgedwongen. Mondriaan gaat op basis van de filterelementen die de gebruiker opgeeft (liefst niet te veel) en de clusters in de opdrachten er ook andere elementen bij betrekken die er iets mee te maken zouden kunnen hebben. Vertrekkende van deze slimme set van elementen worden de combinaties dan gevormd. Men gaat merken dat als een combinatie niet lukt tijdens het plannen dat het kan zijn dat er in die combinatie elementen voorkomen die de gebruiker niet vermeld had in de filter.
Per rooster moet men wat ervaring opdoen om te zien wat het best werkt om problemen op te sporen. We geven hier een aantal tools die dat mogelijk maken zonder harde regels op te leggen.
Combinaties worden geprobeerd van klein naar groot
Van zodra Mondriaan alle te evalueren combinaties opgelijst heeft, wordt geprobeerd ze te plannen (door MBE) in volgorde van klein naar groot (grootte = aantal elementen). Vermits de gebruiker kan opgeven wat de minimale en maximale grootte is, worden ook enkel combinaties die hier aan voldoen weerhouden.
Eerst worden de kleinste combinaties geprobeerd. Voor elk van deze combinaties weet Mondriaan na de test of het een succes was of niet. Stel dat Mondriaan de combinaties van grootte 2 geprobeerd heeft en vaststelt dat combinatie (P,Q) niet succesvol was. In een volgende stap, bij het evalueren van combinaties van grootte 3 gaat Mondriaan alle combinaties van 3 die ook (P,Q) bevatten al schrappen. De combinatie (A,P,Q) wordt dus niet geprobeerd. Dat is immers niet zinvol omdat we al vastgesteld hebben dat (P,Q) niet lukt.
Mondriaan gaat systematisch alle weerhouden combinaties van klein naar groot testen en na elke set (per grootte) eerst een schrapping doen van combinaties uit grotere sets. Op die manier beperken we ook weer het aantal combinaties dat in de analyse moet bekeken worden.
Verder in deze pagina wordt nog uitgelegd waar alle instellingen kunnen gebeuren om deze analyses te doen.
Context waarbinnen de analyse gebeurt
De tool “Analyseer opdrachten” werkt, net zoals “Plan” of “Plan Selectie”, binnen een context van een basisselectie van opdrachten (via elementen) en de settings in volgende gekende optietabbladen:
- Opties voor het roosteren
- Opties voor de MBE
Opties voor het roosteren
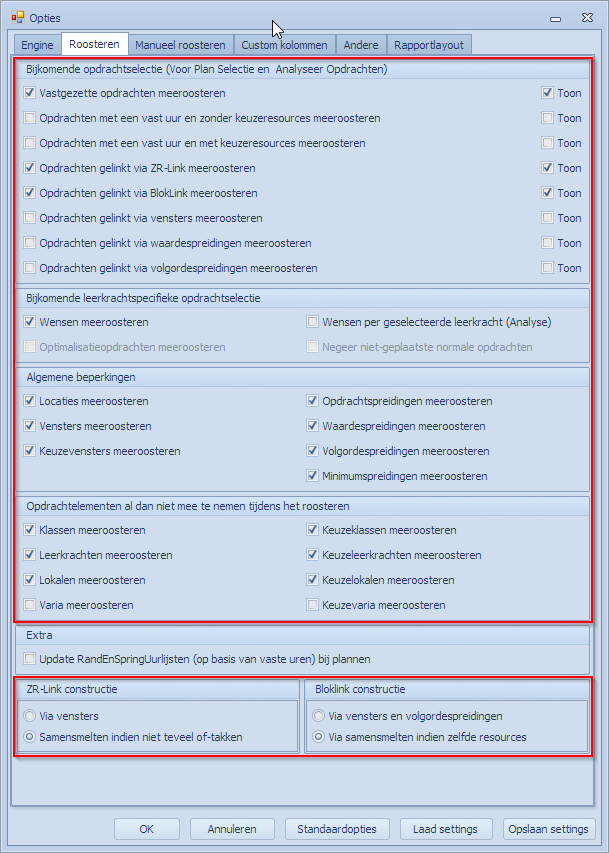
Opties voor het roosteren (Opties | Roosteren): Hier zijn de meeste opties relevant voor “Analyseer opdrachten”.
- Bijkomende opdrachtselectie: Voor elke combinatie van elementen die geanalyseerd moet worden, worden eerst de opdrachten geselecteerd op de manier die hiervoor beschreven werd. Aan deze opdrachten worden vervolgens nog extra opdrachten toegevoegd zoals gesteld in “Bijkomende opdrachtselectie”. Deze volledige set van opdrachten zal naar de MBE gestuurd worden.
- Bijkomende leerkrachtspecifieke opdrachtselectie: Ook de wensen kunnen aan elke combinatie toegevoegd worden. “Optimalisatie” heeft hier geen zin en gebruiken we niet. Er zijn 3 mogelijkheden voor de wensen:
- Men neemt ze niet mee in de analyse.
- Men neemt alle wensen van alle leerkrachten steeds mee voor elke combinatie die geanalyseerd wordt.
- Men neemt per combinatie enkel de wensen mee van de leerkrachten die expliciet geselecteerd worden in de combinatie.
- Algemene beperkingen: Ook deze worden meegenomen in de analyse van elke combinatie.
- Opdrachtelementen al dan niet mee te nemen tijdens het roosteren: Ook aan deze voorwaarden wordt voldaan tijdens de analyse. Merk op dat het niet is omdat we bijvoorbeeld “Klassen meeroosteren” uitvinken dat het systeem van het vormen van combinaties op basis van klassen niet meer zou werken. Dit staat los van elkaar. Selecties en het maken van combinaties worden niet beïnvloed door deze settings. Enkel als de opdrachten naar de MBE gestuurd worden zal deze de instructie krijgen om niet naar de klassen te kijken tijdens het zoeken naar een oplossing.
- ZR-Link/Bloklink constructie: ook hier van toepassing.
Opties voor de MBE
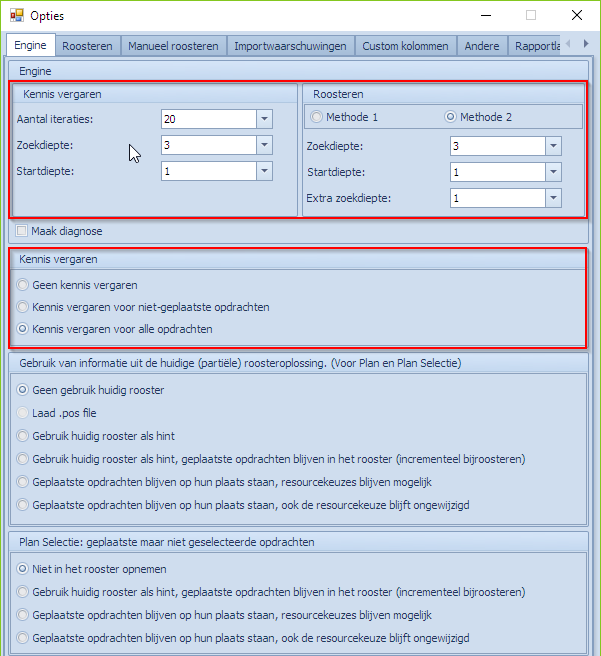
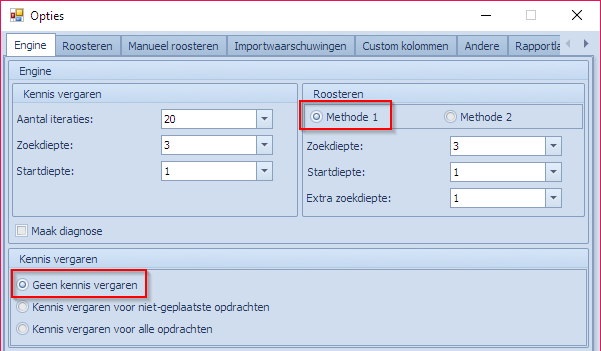
Opties voor de MBE (Opties | Engine): vooral de opties i.v.m. kennis vergaren en de te gebruiken methode zijn hier van belang.
Enkel de eerste 2 blokken uit dit optietabblad zijn ook relevant voor “Analyseer opdrachten”. Zie algemene pagina over dit thema.
Enkele vrijblijvende tips over deze opties
Indien men kleine deelverzamelingen van opdrachten en beperkingen gaat analyseren:
- kan het nuttig zijn om lagere zoekdieptes te gebruiken. Gebruikt men bijvoorbeeld zoekdiepte 3 voor het volledige rooster dan kan men voor de analyse bijvoorbeeld zoekdiepte 2 gebruiken. Als een klein deelprobleem niet of moeilijk op te lossen is op zoekdiepte 2 maakt dit deelprobleem misschien weinig kans om opgelost te worden binnen de context van het volledige rooster op diepte 3.
- zouden deze opdrachten misschien oplosbaar moeten zijn met Methode 1. Dezelfde redenering geldt als voor de zoekdiepte. Een klein probleem zou oplosbaar moeten zijn met de eenvoudige Methode 1.
- zouden deze opdrachten misschien oplosbaar moeten zijn zonder kennis te vergaren.
Dit is echter een kwestie van keuze en ervaring. Men kan ook gewoon de instellingen gebruiken die men gebruikt tijdens het roosteren.
Openen van de analysetool
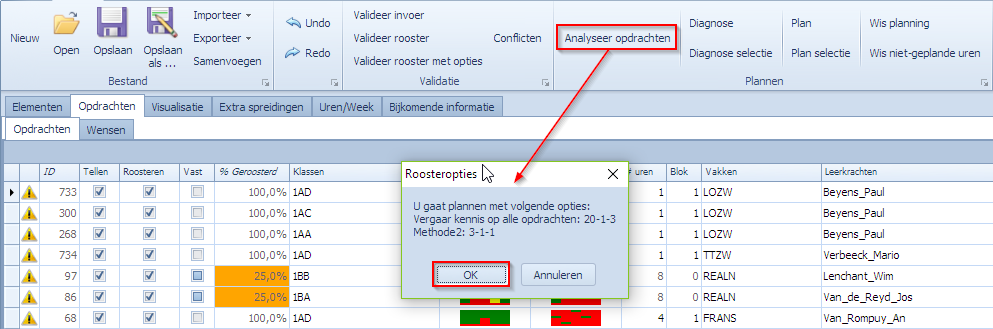
Via het menu “Start | Plannen | Analyseer opdrachten” start men de analysetool op. Eerst wordt een kleine popup getoond met de gekozen MBE opties voor het plannen van de combinaties.
Drukt men op OK, dan komt men in de analysetool:
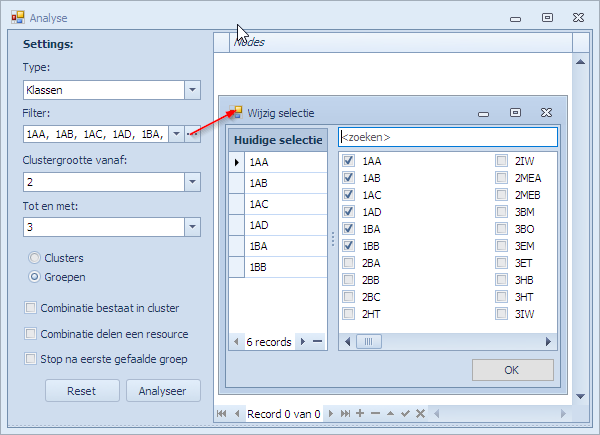
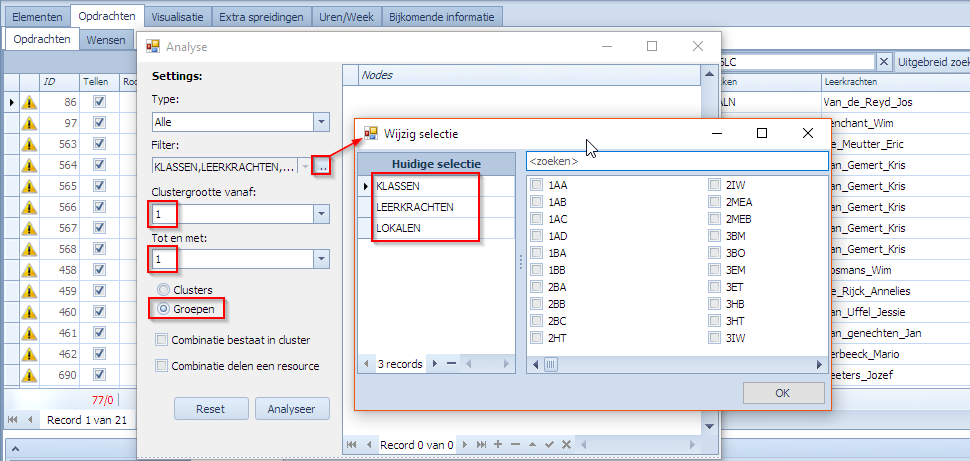
Ter voorbereiding van de analyse kan men volgende instellingen doen in dit scherm:
- Filter: In het veld “Filter” kan men een selectie maken van elementen (en elementgroepen) die gebruikt zullen worden om combinaties te maken. In het voorbeeld tonen we ook het “Wijzig selectie” scherm waarmee de elementen geselecteerd kunnen worden. Merk op dat het veld “Type” bepaalt wat in dit selectiescherm getoond wordt.
- Type: Omdat er erg veel elementen zijn die in het veld “Filter” geselecteerd kunnen worden, kunnen we dit handig beperken door eerst een elementtype in te geven. Mogelijkheden zijn:
- Alle: bij deze keuze kan je in het Filter alle mogelijke elementen en groepen kiezen die er bestaan.
- Klassen: alle klassen en klasgroepen
- Leerkrachten: alle leerkrachten en leerkrachtgroepen
- Lokalen: alle lokalen en lokaalgroepen
- Vakken: alle vakken en vakgroepen
- Clustergrootte vanaf: minimale grootte van de combinaties die getest moeten worden.
- Tot en met: maximale grootte van de combinaties die getest moeten worden.
- Clusters/Groepen: De keuze tussen de “Groepen” methode of de “Cluster” methode om op basis van de opgegeven elementen combinaties samen te stellen die getest moeten worden. Zie eerder in deze pagina voor een uitgebreide beschrijving van de verschillen tussen deze technieken.
- Extra opties voor de “Groepen”-techniek:
- Combinatie bestaat in cluster: enkel combinaties weerhouden als die combinatie als cluster bestaat in minstens één willekeurige opdracht.
- Combinatie delen een resource: enkel combinaties weerhouden waarvan alle elementen met minstens één gemeenschappelijke resource in contact staan via willekeurige opdrachten. (zie eerder op deze pagina voor de uitleg.)
- Stop na eerste gefaalde groep: indien men de analyse wenst te stoppen van zodra de MBE een gefaalde groep of cluster gevonden heeft dan kan men deze optie aanvinken. Vinkt men dit niet aan dan blijft Mondriaan de MBE aansturen tot alle gevraagde combinaties geprobeerd werden.
Knoppen:
- Analyseer: start een analysesessie met de ingegeven parameters.
- Reset: alle settings van het Analysescherm worden weer naar de default settings gezet. De inhoud van “Nodes” waar de probleemcombinaties opgelijst staan, wijzigt uiteraard niet. Verder onthoudt Mondriaan ook per Type de Filter-waarden die laatst gekozen werden. Had men als Type “Klassen” gekozen en als klassen A en B, dan zal dit na een reset onthouden blijven. Kiest men na Reset weer Klassen dan zal Filter gevuld zijn met A en B en kan de gebruiker hier mee verder werken of dit aanpassen.
Overlopen van enkele “Analyseer opdracht” technieken
In dit voorbeeld selecteren we 10 klassen van het 6de jaar. We kiezen vervolgens om te analyseren volgens de “Groepen”-techniek. Als minimale combinatie grootte kiezen we 1 en als maximale 3. Omdat er 10 klassen zijn kunnen we in het geval van “Groepen” de maximale grootte opdrijven tot 10 maar hier kiezen we 3. Verder hebben we in de optietabbladen “Opties | Roosteren” en “Opties | Engine” de standaardopties gekozen.
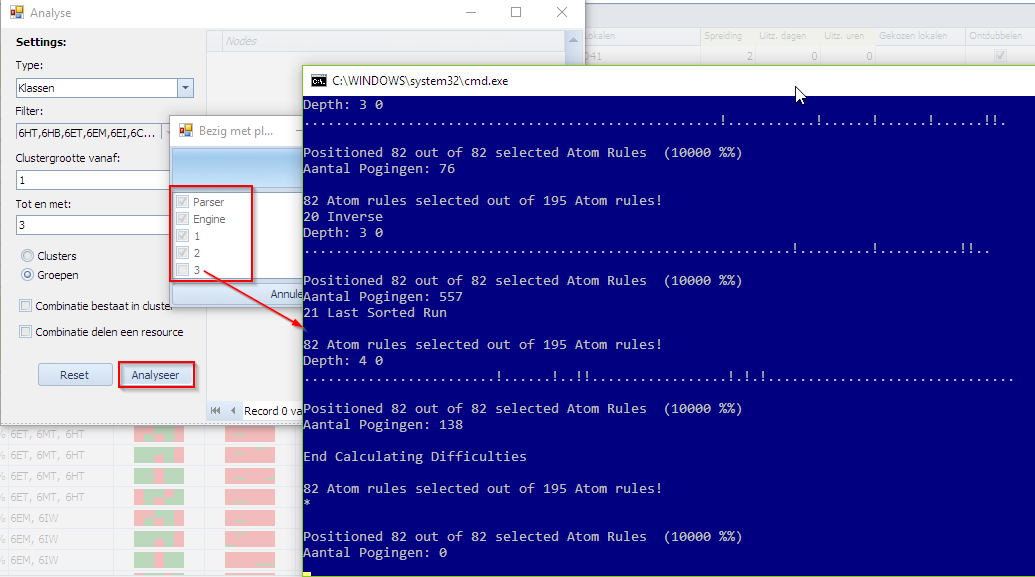
Drukken we vervolgens op “Analyseer”, dan krijgen we volgend beeld te zien tijdens de analyse. Het voortgangsscherm laat zien waarmee Mondriaan bezig is:
- Parser: opstellen en doorsturen van de analyse input aan de MBE (klaar)
- Engine: opstarten van de MBE met de analyseopdrachten (klaar)
- 1: Combinaties van 1 elementen worden geanalyseerd (klaar)
- 2: Combinaties van 2 elementen worden geanalyseerd (klaar)
- 3: Combinaties van 3 elementen worden geanalyseerd (bezig…)
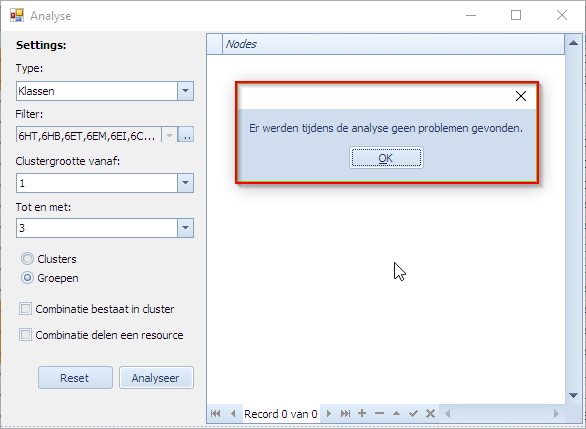
Indien Mondriaan geen problemen gevonden heeft bij het analyseren van deze combinaties, krijgt men het volgende beeld te zien:
Opzoeken van knelpunten door de MBE minder zoekvrijheid te geven
We passen de opties in “Opties | Engine” aan op de volgende manier:
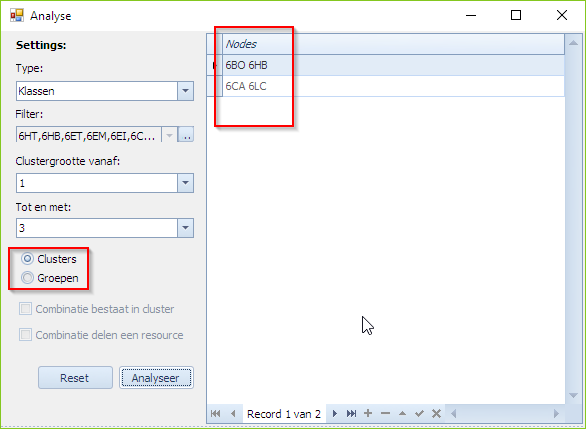
Hierdoor gaat de MBE veel minder “moeite” doen om naar een oplossing te zoeken voor elke combinatie die hij moet analyseren. Drukken we vervolgens opnieuw op de “Analyseer” knop in het Analyse scherm dan krijgen we volgend beeld te zien. Volgende 3 combinaties geven problemen binnen de huidige set aan parameters:
- (6BO, 6HB)
- (6CA, 6LC)
- (6HT, 6IW, 6MT)
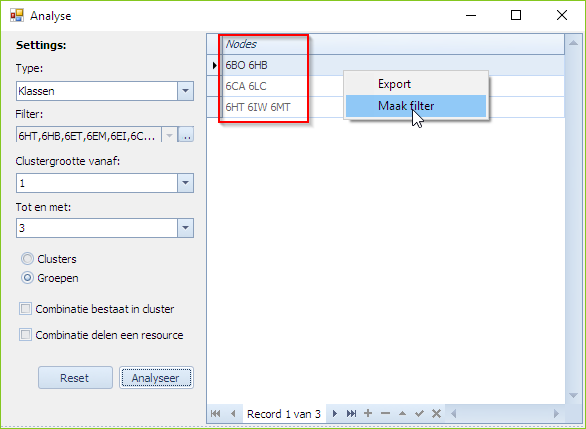
Een gefaalde combinatie gebruiken als filter voor bijvoorbeeld Plan Selectie
Selecteren we de eerste gefaalde combinatie (6BO,6HB), dan kunnen we er via een rechtermuisklik een filtercriterium van maken voor “uitgebreid zoeken” in het opdrachten tabblad. De actie “Maak filter” doet dat en navigeert dan ook meteen naar het opdrachten tabblad.
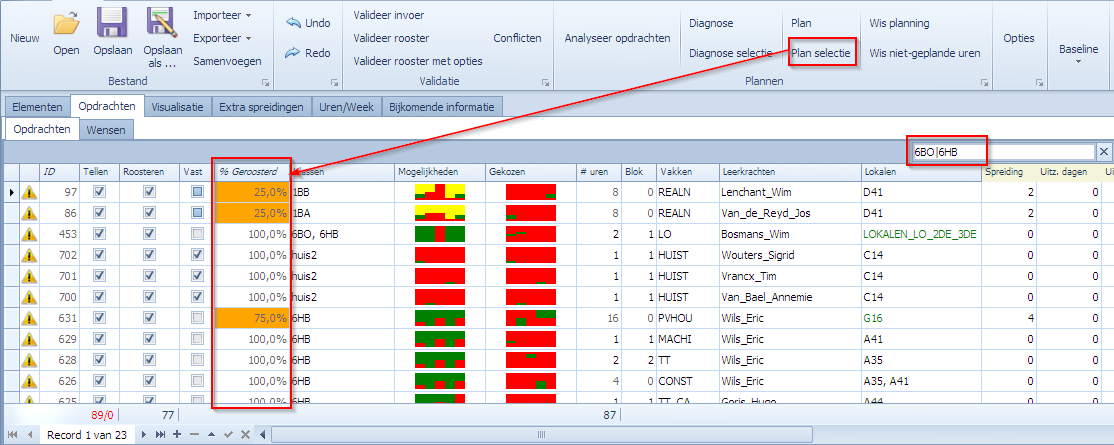
Indien we met deze selectie en dezelfde “Opties | Roosteren” en “Opties | Engine” als voor het analyseren van opdrachten (dus in dezelfde context) een “Plan Selectie” doen van deze selectie, dan zou het resultaat inderdaad moeten zijn dat het niet gepland kan worden. We voeren “Plan Selectie” uit:
Er is inderdaad 1 opdracht die in deze context niet geplaatst kon worden. Maar, omdat we in dit geval weten dat het zeker oplosbaar is als we bijvoorbeeld naar Methode 2 zouden overstappen, of kennis vergaren zouden aanzetten, is het gewoon een indicatie dat het een wat lastigere combinatie is. Merk op dat in dit voorbeeld de eerste 2 opdrachten waar “25% geroosterd” bij staat niet gaat over gefaalde opdrachten. Dit zijn 2 opdrachten waarvan een deel “vast” is en meegeroosterd werd. Het gaat om 1ste jaars. Enkel die 25% is dus mee naar de MBE gegaan. Voor ons gaat het hier vooral om die opdracht van 6HB die niet geplaatst werd.
Opgepast met de optie “Wensen per geselecteerde leerkracht (Analyse)”
“Plan selectie” maakt momenteel geen gebruik van deze optie. Enkel “Analyseer opdrachten” gebruikt die. Als “Wensen meeroosteren” aangevinkt is dan zal “Plan selectie” altijd ALLE leerkrachtwensen meenemen, onafhankelijk van de geselecteerde leerkrachten tijdens “Plan selectie”. Indien men dus een verschil ziet tussen de analyse van een combinatie en een Plan selectie van ogenschijnlijk dezelfde combinatie dan kan dat hier aan liggen.
Mocht er in de toekomst nood zijn om de optie “Wensen per geselecteerde leerkracht” ook van toepassing te laten zijn voor “Plan selectie” dan zullen we dat zeker aanpassen. Nu kan men trouwens ook hetzelfde effect bekomen door in het Wensen tabblad enkel de wensen actief te maken die men wenst te plannen.
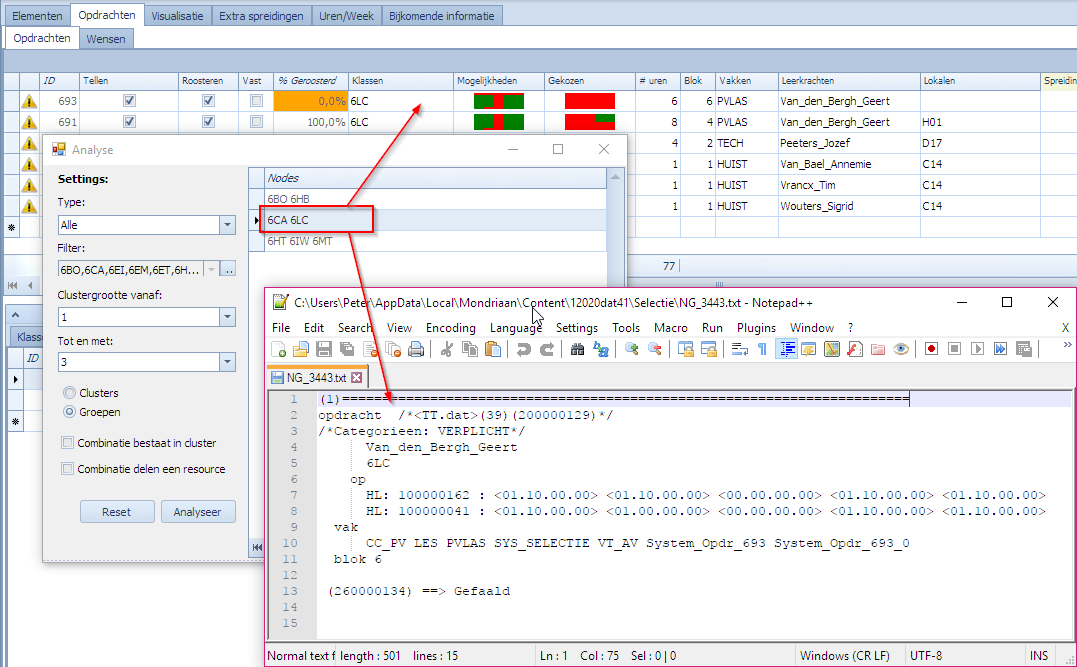
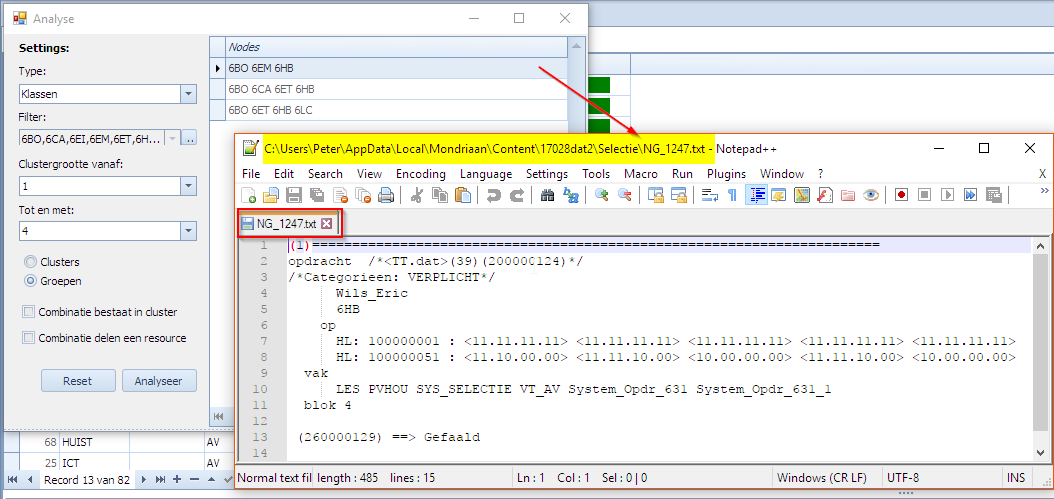
Dubbelklik op een gefaalde combinatie toont de gefaalde opdrachten
In het Analyse scherm kan men dubbelklikken op een gefaalde combinatie. Dit opent een tekstbestand met de gefaalde opdrachten voor die combinatie. Voor de combinatie (6CA,6LC) gaat het om één gefaalde opdracht, een blok van 6 uur. In volgend beeld tonen we die gefaalde opdracht en op de achtergrond wordt ook meteen het resultaat getoond dat we bekomen hadden door een “Plan selectie” te doen met dezelfde gefaalde combinatie. Hier ziet men dus inderdaad dat een “Plan selectie” van dezelfde combinatie in dezelfde context exact hetzelfde resultaat geeft als wat de MBE als resultaat had bij “Analyseer opdrachten”.
Minder combinaties proberen door de “Cluster”-techniek
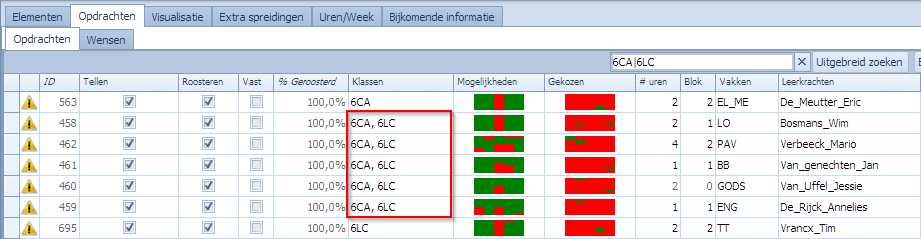
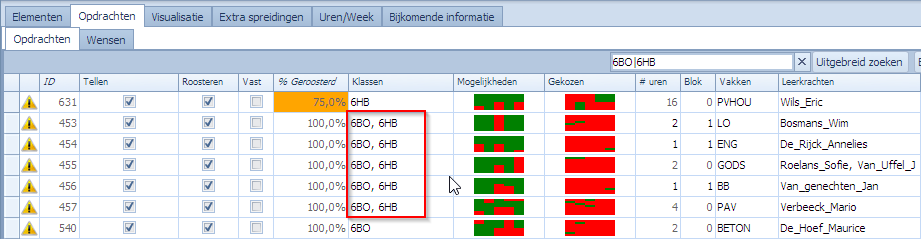
Herhalen we hetzelfde voorbeeld maar met de “Cluster”-techniek dan zien we in dit geval dat de maximale combinatiegrootte niet 10 is maar maximum 3. De reden is dat Mondriaan binnen de 10 geselecteerde klassen maximaal 3 elementen ziet die in eenzelfde opdracht voorkomen. We kiezen min 1 en max 3 en drukken op de “Analyseer” knop:
Dit is veel sneller klaar dan bij de “Groepen”-techniek. Wat onmiddellijk opvalt, is dat er maar 2 combinaties gevonden werden die een knelpunt vormen in de gestelde context. De reden hiervoor is dat de combinatie (6HT,6IW,6MT) nergens voorkomt als cluster in een opdracht. Deze combinatie van elementen werd dus ook niet geprobeerd. De andere 2 combinaties werden wel geprobeerd en komen er uit als knelpunten. Dat ze samen in opdrachten voorkomen kan men in het opdrachten tabblad duidelijk zien:
Teveel combinaties analyseren
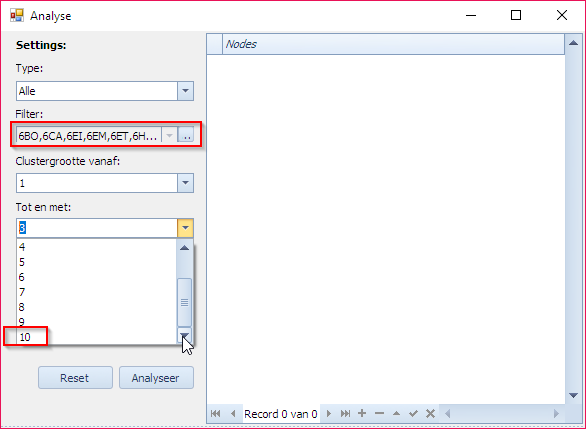
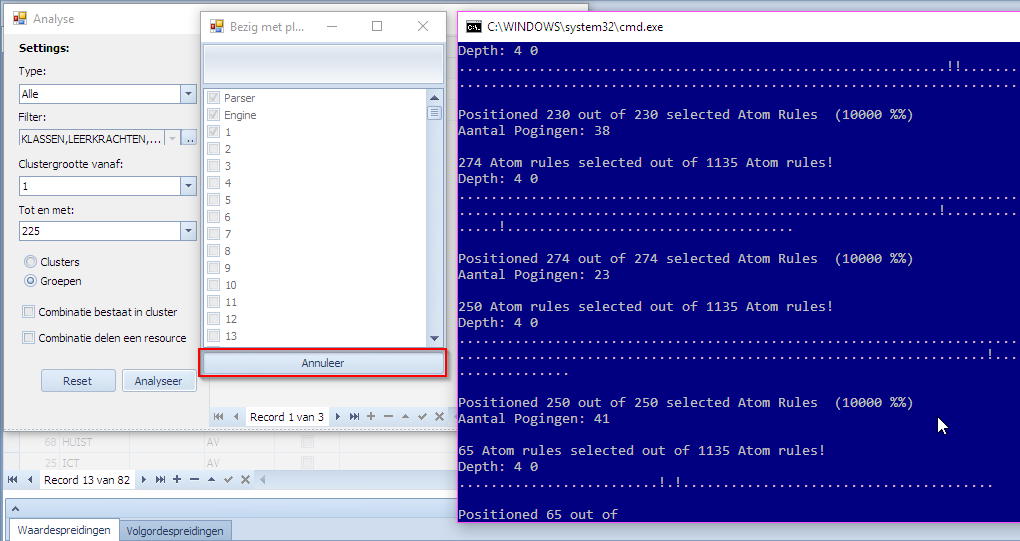
Het is niet moeilijk om in te zien dat men zaken kan vragen die niet echt uitvoerbaar zijn. In theorie kan men bijvoorbeeld voor 100 elementen alle combinaties van grootte 1 tot 100 uitproberen. Dit is niet echt zinnig maar Mondriaan en de MBE zullen niet weigeren om dit uit te voeren. De gebruiker zal snel vaststellen dat hij iets gevraagd heeft wat onzinnig is. Het enige wat er dan opzit, is om de analyse af te breken. In dit voorbeeld hebben we de onmogelijke opdracht gegeven om van de 225 opgegeven elementen alle combinaties groottes uit te proberen van 1 tot 225. De enige manier om dit te stoppen is door op de knop “Annuleer” te klikken.
Drukt men op “Annuleer” dan stopt Mondriaan met het geven van instructies aan de MBE. Het kan echter zijn dat de MBE zelf niet stopt. Als dat het geval is, kan men de MBE zelf gewoon afbreken door op het klassiek kruisje te klikken rechtsboven in het blauwe scherm.
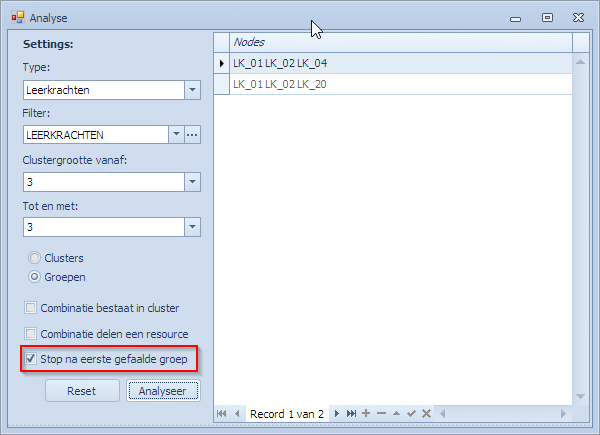
Analyse stoppen na eerst gefaalde groep
Wenst men de analyse te stoppen na de eerste faling die de MBE tegenkomt dan dat dat door de optie “Stop na eerste gefaalde groep” te kiezen. De MBE wordt dan afgebroken en krijgt de gebruiker de controle terug.
Analyseer Individueel
Een veelgebruikte techniek om te zien of het rooster op zijn meest elementaire manier al roosterbaar is, is om het rooster te maken van elke resource afzonderlijk. Kan men voor elke klas, elke leerkracht, elk lokaal, etc. de opdrachten gepland krijgen? Dat is het minste wat men kan verwachten alvorens men begint te roosteren. De tool “Analyseer opdrachten” leent zich uitstekend om dit te onderzoeken. Men selecteert de resources waarvoor men dit wenst te doen, men kiest de “Groepen”-techniek en men selecteert 1 voor zowel de minimale als de maximale combinatiegrootte.
In dit voorbeeld hebben we de standaardgroepen KLASSEN, LEERKRACHTEN, en LOKALEN geselecteerd. Dit kan enkel tegelijkertijd indien men als Type “Alle” gekozen heeft. Vervolgens drukken we op “Analyseer” om voor elke klas, elke leerkracht, en elk lokaal de opdrachten te selecteren en te roosteren. Uiteraard gebeurt dit ook weer binnen de gestelde context in “Opties | Roosteren” en “Opties | Engine”.
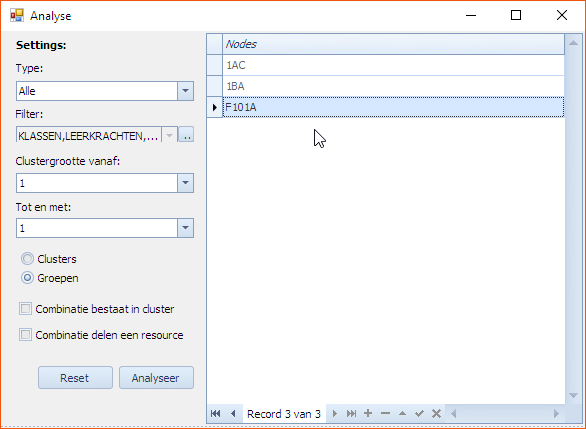
Na uitvoering krijg je bijvoorbeeld volgend beeld waarbij 2 klassen en 1 lokaal een probleem hebben. Opnieuw kan je dan via “Plan Selectie” gaan bekijken wat er mis is met deze individuele resources.
Behouden van de gegevens van een Analyseer Opdrachten
De gegevens van de laatste “Analyseer opdrachten” die te zien zijn in het “Analyse” scherm blijven beschikbaar zolang men ze niet overschrijft door een nieuwe Analyseer opdrachten actie. Ook als men het bestand bewaart en weer opent, blijven deze gegevens beschikbaar.
Het dubbelklikken op een gefaalde combinatie toont normaal een tekstdocument met daarin de gefaalde opdrachten. Deze tekstdocumenten blijven enkel tijdens de Mondriaan sessie beschikbaar. Van zodra men Mondriaan sluit, worden deze gegevens gewist.
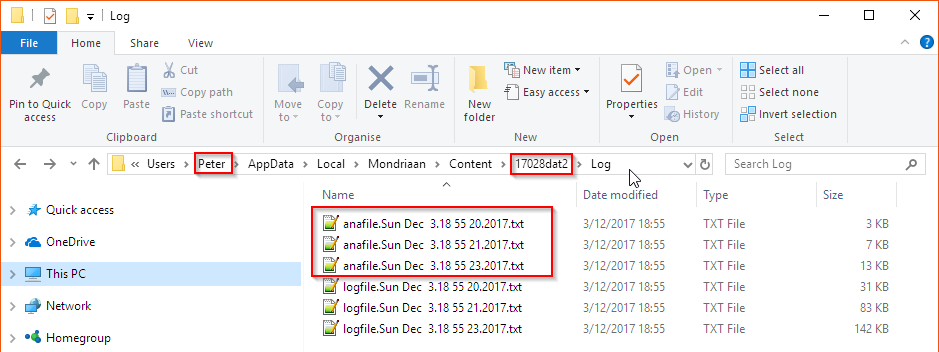
Locatie van tekstbestanden die de MBE aanmaakt bij Analyseer opdrachten
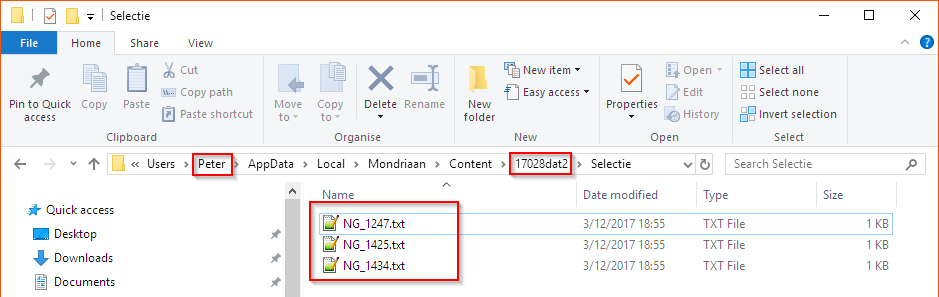
De tekstbestanden die Mondriaan toont als men dubbelklikt op een gefaalde combinatie staan op volgende locatie:
Afhankelijk van de gebruiker (in dit geval “Peter”) moet men onder “Users” (of “Gebruikers”) in de juiste directory kijken. Onder “Mondriaan” vindt men de “Content” map. Daarbinnen wordt elke keer dat de MBE opgestart wordt, een cryptische foldernaam aangemaakt (in dit geval “17028dat2”). Onder deze folder staan subfolders en bestanden die de MBE aanmaakt. Onder “Selectie” kan men de “NG_*.txt” bestanden vinden die tijdens de analyse aangemaakt worden. De link tussen de gefaalde combinatie en het bestand kent alleen Mondriaan.
Extra analysebestanden met statistieken over de uitgevoerde analyse
Soms kan het nuttig zijn om van alle geanalyseerde combinaties, of ze nu slagen of niet binnen de gestelde context, te weten hoe ze zich verhouden tot de andere combinaties voor wat betreft hoe “lastig om op te lossen”. De MBE voorziet hiervoor per “grootte” van de geanalyseerde combinaties een analysebestand (“anafile”). Deze analysebestanden-files kan men op volgende locatie vinden:
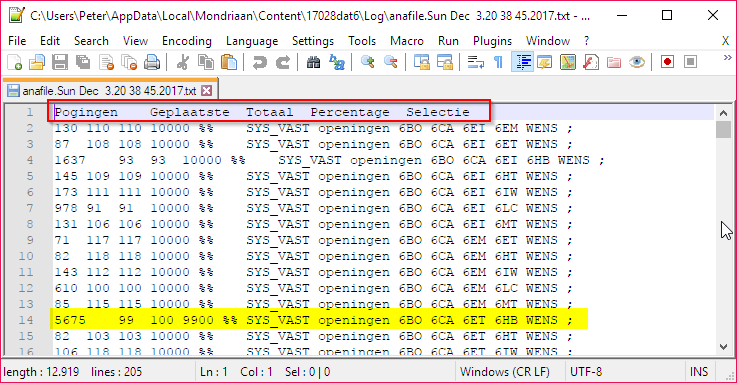
Deze bestanden staan per datum gesorteerd, wat meteen betekent dat ze per grootte van de combinaties gesorteerd zijn. We openen het laatste bestand. Elke lijn stelt een combinatie voor die geanalyseerd werd. Het is duidelijk dat in dit bestand steeds combinaties van 4 elementen opgelijst zijn. We zien volgende kolommen:
- Pogingen: geeft een idee van het aantal “pogingen” die de MBE heeft uitgevoerd om de opdrachten van een bepaalde combinatie te plaatsen.
- geplaatste: aantal geplaatste opdrachten
- Totaal: totaal aantal aangeboden opdrachten voor de combinatie van elementen
- Percentage: percentage geplaatste opdrachten (geplaatst tov totaal)
- Selectie: de selectiecriteria om opdrachten te selecteren voor de combinatie
We kunnen opmaken uit de kolom “Selectie” dat buiten de 4 elementen nog andere opdrachten geselecteerd werden. Zo zien we volgende indicaties:
- “SYS_VAST”: vaste opdrachten worden mee geselecteerd
- “openingen”: vensters worden mee geselecteerd
- “WENS”: alle leerkrachtwensen worden mee geselecteerd
Dit is het resultaat van de standaardopties bij “Opties | Roosteren”. Kiest men andere opties dan zullen er ook andere indicatoren instaan.
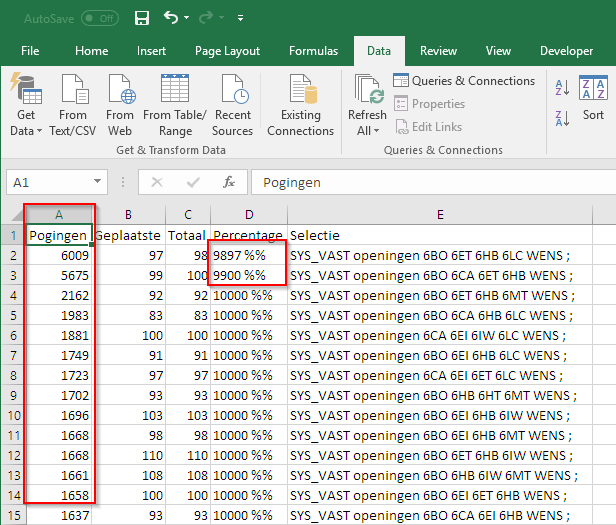
Interessant aan dit bestand is dat het “tab gescheiden” is en dat men het ook eenvoudig kan openen in bijvoorbeeld Excel. Vervolgens kan men de gegevens gemakkelijk sorteren op “Pogingen” waardoor men een goed zicht krijgt op de lastige combinaties. Een voorbeeld hiervan:
Na openen in Excel en omgekeerd sorteren op “Pogingen”, krijgen we zicht op de lastige combinaties van 4 elementen. Voor de opdrachten van de eerste 2 combinaties zien we dat er ook telkens een opdracht gefaald is. Het is logisch dat die dan ook hoog gesorteerd staan. Men ziet ook een duidelijke sprong in het aantal pogingen.
Deze informatie is niet onmiddellijk beschikbaar in Mondriaan zelf, maar de geïnteresseerde gebruiker kan de informatie hier vinden en het kan soms nuttig zijn om een beeld te krijgen van lastige combinaties als men moeilijk oplosbare problemen onderzoekt.